Na figura abaixo, uma barra fina de vidro forma uma semicircunferência de raio .
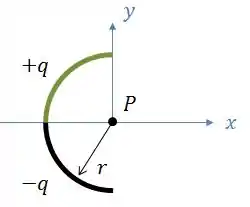
Uma carga está distribuída uniformemente na metade superior da barra, e uma carga está distribuída uniformemente na metade inferior.
Determine:
- O módulo do campo elétrico no ponto , situado no centro do semicírculo.
- A orientação (em relação do semi-eixo positivo) do campo elétrico no ponto , situado no centro do semicírculo.
Passo 1
Nesse tipo de problemas, a malandragem é explorar, logo de cara, a simetria do problema.
Vou começar fazendo o seguinte: vou pegar dois pontos simétricos e ver qual seria o campo elétrico resultante no ponto , decompondo o campo elétrico em componentes e .
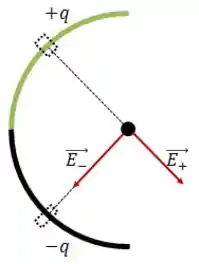
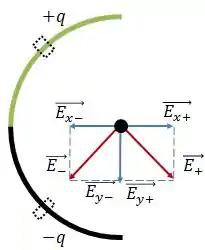
Tá vendo que as componentes em vão se anular e as componentes em vão se somar?
Então, o campo elétrico resultante vai ser algo do tipo:
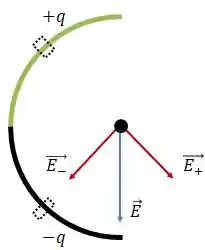
Show de bola! Essa interpretação facilita a nossa vida porque não precisamos mais nos preocupar com uma componente horizontal desse campo elétrico.
A figura mostra também que os dois arcos produzem o mesmo campo elétrico na vertical. Assim, só precisamos calcular um deles.
Passo 2
A contribuição devido a um elemento de carga da haste superior é dada por:
Sabendo que a carga é distribuída uniformemente ao longo da haste, podemos dizer que:
Onde é a densidade linear de carga. Sabendo também que se trata de um arco, podemos dizer que , onde vai variar de a . Portanto:
Entretanto, como estamos interessados somente na componente vertical, vamos precisar decompor esse campo , assim como fizemos antes:
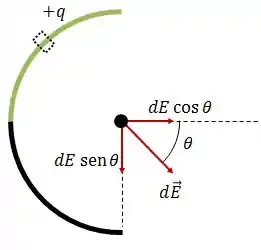
Portanto:
Agora sim, agora estamos falando a minha língua!
Pra calcular o campo elétrico resultante da haste superior, basta integrar isso aqui:
Sabendo que é a densidade linear de carga, podemos dizer que:
Substituindo de volta:
Eita! Eu sei, foi tenso... mas só falta um detalhe pra terminar, juro!
Passo 3
Acontece que calculamos somente o campo elétrico da parte positiva da haste. Mas como sabemos que o campo vertical produzido pela parte negativa vai ser igual, baste dizer que:
Logo:
Agora sim, acabou!
Ah! Caso você tenha usado ao invés de , o resultado que você vai encontrar vai ser
Relaxa, as duas respostas estão certas.
Agora só temos que substituir os valores!
Passo 4
Onde:
;
;
;
;
Logo:
Resposta
- O campo é vertical, apontando para baixo (sentido ).