Um fio e um plano, ambos infinitos, carregados eletricamente, são posicionados paralelamente como ilustrado na figura.
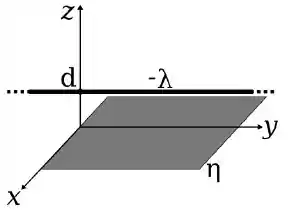
As densidades de carga do fio e do plano valem e , respectivamente, onde e são números positivos. O local onde a intensidade do campo elétrico resultante é nulo:
se localiza em um outro plano (paralelo ao plano carregado) que cruza o eixo na posição .
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .
se localiza em um outro plano (paralelo ao plano carregado) que cruza o eixo na posição .
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .
Passo 1
Analisando o problema de lado, olhando somente o plano , teremos o seguinte:
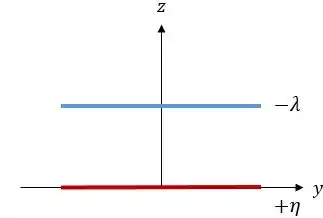
Estamos analisando esse plano pois, somente sobre esse plano as linhas de campo do fio e do plano terão as mesmas direções.
Passo 2
Como o fio está carregado negativamente, as linhas de campo estarão entrando nele. E como o plano está carregado positivamente, as linhas de campo estarão saindo dele, se liga:
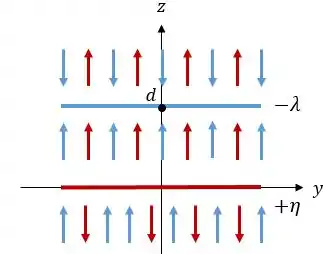
Assim, o campo poderá ser nulo somente no plano ou acima do fio, ou abaixo do plano. Para saber o ponto exato, precisamos avaliar a equação de cada campo.
Passo 3
O campo gerado por um fio infinito de densidade linear de carga é dado por:
Onde é a distância entre o fio e o ponto onde estamos medindo o campo elétrico. Lembra como chega nessa expressão? Vou dar um bizu aqui rápido mas a gente tem isso melhor explicado na teoria!
Esse fio tem simetria cilíndrica, então vamos usar uma gaussiana cilíndrica de raio e comprimento que tem seu eixo coincidindo com o fio. Pela lei de Gauss temos
Só vai ter fluxo não nulo de campo elétrico na área lateral da Gaussiana e esse campo sai normal a essa superfície, assim
Por outro lado, a carga total dentro da gaussiana vai ser a densidade de carga do fio vezes o comprimento do pedaço do fio que tá dentro da gaussiana que é
Assim
Aí quando estamos no plano a direção do campo é a direção , assim
Beleza?
Como o fio está posicionado no ponto , podemos escrever como:
Logo:
E esse campo tá com comportamento certinho, quer ver?
Para a gente vai ter que o campo aponta na direção como no nosso desenho.
Para o denominador lá do campo vai ficar negativo e toda a expressão do campo vai estar positiva, ou seja, apontando na direção . Belezinha?
Passo 4
Já o campo elétrico gerado pelo plano infinito é dado por:
Agora basta avaliar cada região.
Passo 5
Para , somando as expressões dos campos elétricos:
Agora é só arrumar a bagunça.
Opa! Esse resultado é válido, já que esse ponto se encontra acima do fio de cargas.
Passo 6
Para , somando as expressões dos campos elétricos:
Agora é só arrumar a bagunça.
Como o problema somente nos deu a opção que encontramos no Passo 4, a resposta certa é a letra .
Resposta
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .