Considere uma barra finita de comprimento , com densidade linear de carga uniforme .
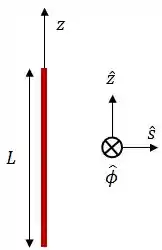
Qual das afirmativas abaixo é verdadeira?
O campo elétrico sempre aponta na direção .
O campo elétrico só depende da coordenada .
A direção do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
Passo 1
O valor do campo pode ser calculado por meio de uma integral a partir de cada componente infinitesimal da barra. Podemos calcular o campo elétrico a partir do cálculo isolado da componente e da componente do mesmo:
Os limites de integração e dependem da posição da barra. De fato, é o ângulo entre o ponto da barra considerado e o ponto onde queremos calcular o campo.
Os limites de integração determinam três casos diferentes:
- Se então o ponto onde queremos calcular o campo passa pela mediana da barra. Ou seja: a barra está numa posição simétrica em relação ao ponto. Nessa situação, temos um campo nulo em , e não nulo em .
- Se a barra estiver mais para cima, temos um campo com uma componente em e uma componente em .
- Caso a barra estivesse mais para baixo, também teríamos uma componente uma componente .
Assim, a coordenada é importante para que calculemos o campo elétrico.
Passo 2
O mesmo ocorre para a coordenada . Para notar isso, vamos tomar o caso em que o ponto considerado se encontra na metade da barra, no caso em que . Claramente, nessa situação, quanto mais próximo o ponto onde calcularemos o campo estiver, maior será o campo elétrico .
Isso aconteceria porque o valor de na integral seria reduzido para cada ponto infinitesimal dessa soma infinita. Isso geraria um aumento significativo no módulo do campo.
Passo 3
A coordenada representa o ângulo ao redor da barra que localiza o ponto considerado. Para valores diferentes de , a barra se encontra à mesma distância da barra mas em orientações diferentes.
Isso não muda o valor do campo pois:
E, por essa razão, alterar não alteraria o valor de nenhum termo da integral:
Isso garantiria o mesmo módulo para o campo elétrico, restando-nos a letra como resposta.
Resposta
O módulo do campo elétrico independe da coordenada .