Um plano condutor infinito e aterrado, ou seja, mantido a um potencial eletrostático zero, é posicionado sobre o plano de um sistema de coordenadas. Uma partícula de carga é posicionada sobre o eixo , na porção , a uma distância do plano, como mostrado na figura abaixo. Sabe-se que, quando o sistema partícula plano está em equilíbrio eletrostático, o campo eletrostático na região é idêntico ao produzido por outro sistema onde o plano é substituído por uma segunda partícula, de carga , colocada na posição correspondente à imagem especular da primeira partícula com relação ao plano.l
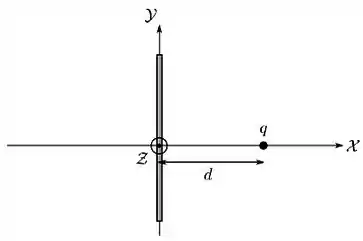
(a) Determine a força eletrostática (módulo, direção e sentido) que o plano exerce sobre a partícula.
(b) Determine o campo eletrostático (módulo, direção e sentido) produzido pelo sistema partícula plano em um ponto arbitrário sobre o plano , a uma distância da origem. Considere que este ponto está na vizinhança externa do plano na porção .
(c) Utilizando o resultado do item anterior, determine a densidade superficial de carga induzida sobre o plano no ponto . Interprete o resultado.
Passo 1
Vamos, inicialmente, analisar o que ocorre na região ao substituirmos o plano por uma partícula de carga posicionada em .
Sabemos que a força eletrostática que o plano exerce sobre a partícula é idêntica à força entre as duas cargas e , separadas por uma distância . Utilizando a lei de Coulomb, temos que:
Essa força tem caráter atrativo, o que indica que deve haver uma indução de cargas negativas sobre o plano.
Passo 2
Utilizando o sistema auxiliar, vemos que o campo eletrostático produzido na vizinhança externa do plano na região será como o de um dipolo elétrico simples. Como esse plano é uma superfície equipotencial, o campo eletrostático deve ser perpendicular a ele e apontar no sentido negativo do eixo .
Além disso, como pontos sobre o plano a uma mesma distância da origem estão equidistantes das duas partículas, vemos que, por simetria, o campo eletrostático deve ser o mesmo nesses pontos. Assim sendo, basta considerarmos um ponto sobre o eixo , como mostrado na figura abaixo.
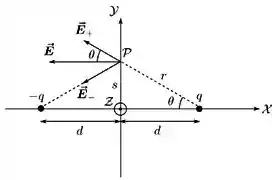
Pelo princípio da superposição, o campo eletrostático resultante deve ser a soma vetorial dos campos produzidos por cada carga. Como o sistema é simétrico, as componentes verticais desses campos se cancelam. Assim sendo, temos que:
Como e , obtemos:
Passo 3
Sabemos que o campo eletrostático na vizinhança externa da superfície de um condutor em equilíbrio é dado por , onde é a densidade superficial de carga do condutor e é o vetor unitário perpendicular à superfície naquele ponto, apontando para fora do condutor.
Na questão, temos que , de modo que a densidade superficial de carga no ponto é dada por:
Bem, vamos analisar o resultado: é não-uniforme e negativa em todos os pontos sobre o plano. Assim sendo, a partícula carregada induz cargas de sinal oposto sobre o plano, dando origem à força atrativa que obtivemos no item (a).
Resposta
(a)
(b)
(c)