A figura abaixo mostra um anel fino de plástico e raio com uma carga uniformemente distribuída.
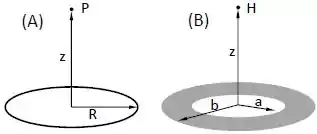
Qual a direção do campo elétrico no ponto da figura , a uma distância do centro do anel ao longo do seu eixo? Justifique sua resposta.
Determine o módulo do campo elétrico no ponto da figura .
A figura mostra um anel de raios interno e externo e , respectivamente. O anel tem densidade superficial de carga uniforme, . Determine o módulo do campo elétrico no ponto , que se encontra sobre o eixo do anel, a uma distância do seu centro.
Dado:
Passo 1
Qual a direção do campo elétrico no ponto da figura , a uma distância do centro do anel ao longo do seu eixo? Justifique sua resposta.
O segredo aqui é explorar a simetria do problema.
Vamos pegar dois pontos dessa circunferência, cada um com carga , e vamos olhar pro campo elétrico gerado por cada uma dessas cargas.
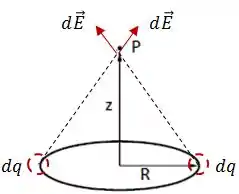
Se decompormos cada vetor, veremos que as componentes horizontais irão se cancelar, e as componentes verticais irão se somar.
Isso vai acontecer para qualquer par de pontos simétricos. O resultado disso é que o campo elétrico resultante terá direção vertical e, como a carga do anel é positiva, terá o sentido apontando para cima.
Passo 2
Determine o módulo do campo elétrico no ponto da figura .
Vamos começar a partir do campo elétrico gerado por um pedaço do anel com carga infinitesimal .
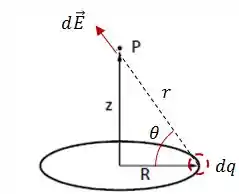
No entanto, como concluímos na letra , o campo elétrico tem direção vertical, apontando para cima. Logo, podemos nos preocupar apenas com a componente do campo elétrico.
Onde:
Sendo o ângulo no plano do anel.
Substituindo esses caras, teremos:
Integrando os dois lados, teremos:
A densidade linear de carga é dada por:
Substituindo, teremos:
Finalmente:
Passo 3
A figura mostra um anel de raios interno e externo e , respectivamente. O anel tem densidade superficial de carga uniforme, . Determine o módulo do campo elétrico no ponto , que se encontra sobre o eixo do anel, a uma distância do seu centro.
Dividindo o disco em anéis concêntricos com espessura infinitesimal, o campo elétrico gerado por cada anel de carga será:
Utilizando o conceito de densidade superficial de carga, podemos dizer que:
Logo:
Integrando dos dois lados:
O enunciado já nos deu a resposta dessa integral:
Onde:
Finalmente:
Agora é só organizar a bagunça:
Jogando o sinal negativo pra dentro dos colchetes, teremos:
Resposta
O campo elétrico terá direção vertical, apontando para cima.