A figura abaixo mostra uma barra retilínea não condutora de comprimento , com carga elétrica uniformemente distribuída.

Qual é a densidade linear de carga da barra?
Calcule o vetor campo elétrico produzido no ponto , situado no eixo , a uma distância da extremidade direita da barra, em termos das variáveis dadas no problema.
Considere que no ponto seja colocado um dipolo elétrico, de momento de dipolo elétrico de módulo , formando um ângulo de com o eixo positivo. Calcule a energia potencial do dipolo.
Passo 1
Qual é a densidade linear de carga da barra?
A densidade linear de carga é definida por:
Como a carga está uniformemente distribuída, a densidade linear de carga será dada por:
Passo 2
Calcule o vetor campo elétrico produzido no ponto , situado no eixo , a uma distância da extremidade direita da barra, em termos das variáveis dadas no problema.
Vamos começar escrevendo o campo gerado por um pedaço infinitesimal da barra com carga .
Como vimos no Passo 1, a carga pode ser escrita como:
Onde a variável é definida a partir da origem. Assim, a relação entre as coordenadas e é representada na imagem abaixo:
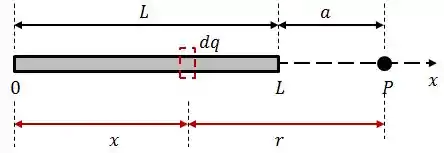
Substituindo isso na expressão de , teremos:
Onde . Agora basta integrar esse cara.
Passo 3
Podemos fazer essa integração por substituição, onde:
Assim, teremos:
Substituindo de volta e colocando os limites de integração, teremos:
Agora é só arrumar a bagunça:
Onde . Assim, finalmente teremos:
Como a carga é positiva, o campo elétrico vai apontar no sentido positivo do eixo .
Passo 4
Considere que no ponto seja colocado um dipolo elétrico, de momento de dipolo elétrico de módulo , formando um ângulo de com o eixo positivo. Calcule a energia potencial do dipolo.
Vamos começar visualizando a situação:
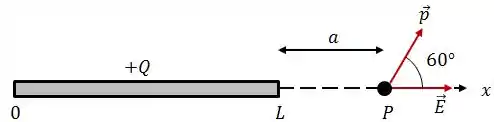
A energia potencial de um dipolo elétrico é dado por:
Substituindo a expressão do campo elétrico que encontramos na letra , teremos:
Resposta