Uma barra isolante uniformemente carregada com carga é dobrada em forma de um quarto de círculo como mostra a figura.
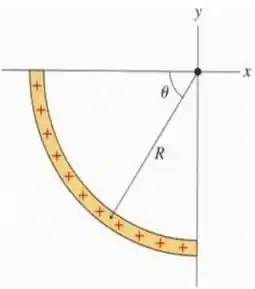
![]()
(a)
(b)
(c)
(d)
(e)
Passo 1
Escrever a componente infinitesimal de campo elétrico em :
Passo 2
Alterar a equação do passo , escrevendo em função de , que é a variável que vamos usar para integrar.
é a densidade linear da barra, que é constante. é o pequeno comprimento da barra. O compomento total da barra vale:
Onde é o ângulo em radianos. Logo: .
Por isso:
Mas a densidade linear, por ser constante, é igual à divisão entre a carga total e o comprimento total do cargo:
Então:
Passo 3
Substituir o resultado do passo no passo e integrar:
Rearrumando:
Agora é integrar e jogar quem é constante para fora da integral:
Resposta
Letra (c):