Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 4123567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

Na figura abaixo, uma barra não condutora “semi-infinita” (ou seja, infinita apenas em um sentido) possui uma densidade linear de cargas uniforme λ .

Mostre que o campo elétrico E P → no ponto P faz um ângulo de 45 ° com a barra e que esse resultado não depende da distância R .

(Sugestão: Calcule separadamente as componentes de E P → nas direções paralela e perpendicular à barra.)

Passo 1

Ok, vamos seguir a sugestão do problema!

Obs: Nesse tipo de problema, calcular as componentes separadamente é sempre o melhor caminho, então guarda isso contigo!

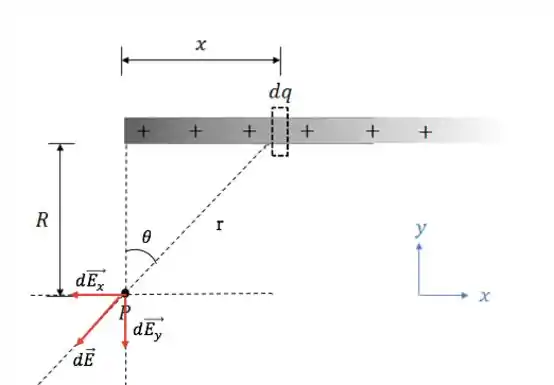
Pra fazer isso, vamos pegar um pedaço infinitesimal da barra com carga d q e calcular as componentes do campo elétrico gerado por ela ( d E x e d E y ) no ponto P .

Olhando a figura, podemos dizer que

d E x = - d E sen ⁡ θ = - d q 4 π ε 0 r 2 sen ⁡ θ

d E y = - d E cos ⁡ θ = - d q 4 π ε 0 r 2 cos ⁡ θ

Sabemos ainda que:

d q = λ d x

Logo:

d E x = - λ d x 4 π ε 0 r 2 sen ⁡ θ

d E y = - λ d x 4 π ε 0 r 2 cos ⁡ θ

Nessas equações, tanto x quanto r quanto θ vão variar quando formos integrar, então precisamos deixar tudo em função de uma única variável.

Passo 2

Vamos lá! Temos que relacionar θ ,   r e x . Como podemos fazer isso?

Bom, pela figura, podemos chegar que:

c o s θ = R r → r = R c o s θ

t g   θ = x R → x = R   t g θ → d x = R s e c θ 2 d θ = R c o s θ 2 d θ

Substituindo esses resultados em nossas equações de d E x e d E y :

d E x = - λ R 4 π ε 0 R c o s θ 2 c o s θ 2 sen ⁡ θ = - λ 4 π ε 0 R sen ⁡ θ d θ

d E y = - λ d x 4 π ε 0 r 2 cos ⁡ θ = - λ 4 π ε 0 R cos ⁡ θ d θ

Passo 3

Último passo, galera!!

Agora, temos que integrar. Como queremos pegar a barra toda e ela é semi-infinita, vamos integrar com θ variando de 0 a π / 2 :

d E x = - λ 4 π ε 0 R sen ⁡ θ d θ

E x = - λ 4 π ε 0 R ∫ 0 π 2 sen ⁡ θ d θ = λ 4 π ε 0 R cos ⁡ π 2 - cos ⁡ 0 = λ 4 π ε 0 R 0 - 1

E x = - λ 4 π ε 0 R

E o campo na direção y fica

d E y = - λ 4 π ε 0 R cos ⁡ θ d θ

E y = - λ 4 π ε 0 R ∫ 0 π 2 cos ⁡ θ d θ = - λ 4 π ε 0 R s e n π 2 - s e n 0 = - λ 4 π ε 0 R 1 - 0

E y = - λ 4 π ε 0 R

Percebemos, então que E x = E y , independente do valor de R . Logo, temos que o ângulo entre o campo e a barra é θ = 45 ° .

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri