Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 4312345678910111213141516171819202122232425262728293031323334353637383940414244454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

Campo Elétrico

Seja λ a carga por unidade de comprimento distribuída uniformemente ao longo de um segmento de reta de comprimento L .

Determine:

  1. O vetor campo elétrico em um ponto P , situado a uma distância a de uma das extremidades do segmento carregado, e situado sobre o seu prolongamento;
  2. A aceleração que uma partícula, de massa m e carga q , sofre quando colocada no ponto P .

Passo 1

  1. O vetor campo elétrico em um ponto P , situado a uma distância a de uma das extremidades do segmento carregado, e situado sobre o seu prolongamento;

    2. Beleza!

    Pra resolver esse tipo de problema, vamos começar pegando, da barra, uma pedaço infinitesimal de carga d q e ver o campo elétrico produzido por ela.

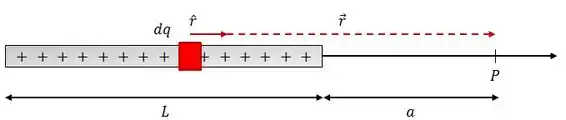
    O campo elétrico gerado pelo elemento de carga d q é dado por:

    d E → = d q 4 π ϵ 0 r 2   r ^

    Passo 2

    Antes de voltarmos pra fórmula, repara que a carga infinitesimal d q pode ser escrita em função da densidade linear de carga λ .

    d q = λ d r

    Agora sim!

    Passo 3

    d E → = λ d r 4 π ϵ 0 r 2   r ^

    Agora é só integrar esse cara, onde:

    a ≤ r ≤ a + L

    Logo:

    E → = λ 4 π ϵ 0   ∫ a a + L d r r 2   r ^

    E → = λ 4 π ϵ 0   - 1 r a a + L r ^

    E → = λ 4 π ϵ 0   1 a - 1 a + L r ^

    E → = λ 4 π ϵ 0 L a a + L r ^

    E → = λ L 4 π ϵ 0 a ( a + L ) r ^

    Ah! Ao invés de r , você poderia ter usado x também... não tem problema. Só procura desenhar o vetor pra especificar o jeito como você está usando ele.

    Passo 4

  2. A aceleração que uma partícula, de massa m e carga q , sofre quando colocada no ponto P .

Vambora! A força que age sobre a carga q é proveniente do campo elétrico E → . Assim, pela segunda lei de Newton.

m a → = q E →

Onde F → e l = q E → . Logo:

a → = q m E →

a → = q m   λ L 4 π ϵ 0 a ( a + L ) r ^

a → = λ L q 4 π ϵ 0 m a ( a + L ) r ^

Resposta

a.

E → = λ L 4 π ϵ 0 a ( a + L ) r ^

b.

a → = λ L q 4 π ϵ 0 m a ( a + L ) r ^

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri