a) Uma haste infinita, isolante e de raio desprezível, possui uma densidade linear de carga . Calcule o vetor campo elétrico a uma distância radial r medida desde o eixo da haste.
Passo 1
Nesse problema a gente tem algo parecido com o que mostra a figura a seguir
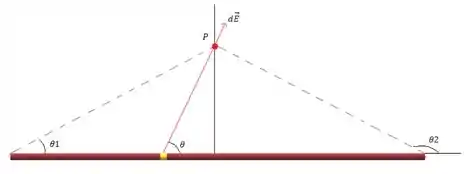
Em uma haste infinita, a distância entre as extremidades e o ponto onde iremos calcular o campo elétrico é muuuito grande, isso quer dizer que, na figura, e .
O campo elétrico em um ponto devido a uma haste de comprimento finito carregada é
Onde
Então vamos tomar os limites de e nas expressões acima para encontrarmos o campo elétrico gerado por uma haste infinita.
Passo 2
Começando por
Agora para
Então, temos que
Resposta
Exercícios de Livros Relacionados
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri