Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 8312345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182848586

Enunciado

O campo elétrico sobre o eixo de simetria (eixo z ) de um anel de raio r e carga total Q > 0 é dado por

E → a n e l = 1 4 π ϵ 0 Q z r 2 + z 2 3 / 2   k ^

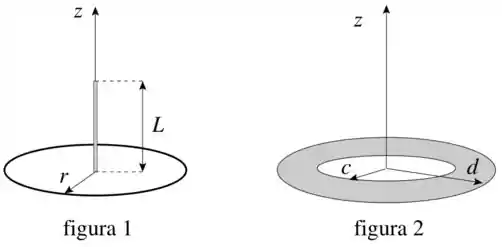
(a) Calcule a força elétrica que o anel exerce sobre um fio retilíneo de comprimento L e densidade linear de carga λ > 0 , posicionado sobre o eixo z , conforme a figura 1 .

(b) Calcule o campo elétrico sobre o eixo de simetria (eixo z ) de um disco vazado com raio interno c e raio externo d , carregado com uma densidade superficial de carga uniforme σ > 0 , conforme a figura 2.

Passo 1

Já temos pelo enunciado o campo gerado por um anel, o que é um grande alívio!

A fórmula dada pelo enunciado já está toda direitinha para usarmos pois é o campo gerado por todo o anel em um ponto do eixo z (que passa pelo seu centro) e que está a uma distância z do centro do anel.

Agora temos que calcular a força que esse anel exerce sobre o fio que está no eixo z . O que acontece aqui é que para cada pedacinho desse fio haverá a seguinte força

d F → f i o = d q f i o E → a n e l

Esse pedacinho de carga tá destacado na figura.

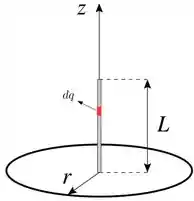
Esse pedaço de fio terá um comprimento d z e como a sua densidade linear de carga é λ , temos

λ = d q f i o d z → d q f i o = λ d z

Assim, a força sobre esse pedaço de fio será

d F → f i o = λ d z E → a n e l

Usando a expressão do campo dada pelo enunciado

d F → f i o = λ d z 1 4 π ϵ 0 Q z r 2 + z 2 3 / 2   k ^

Passo 2

Agora para calcular a força total sobre o fio, temos que levar em conta a contribuição de cada pedacinho do fio.

Isso é feito integrando a equação anterior de 0 a L em z (ou seja, ao longo do fio)

F → f i o = ∫ 0 L λ d z 1 4 π ϵ 0 Q z r 2 + z 2 3 / 2   k ^

F → f i o = λ Q k ^ 4 π ϵ 0 ∫ 0 L d z z r 2 + z 2 3 / 2  

Essa integral meio chatinha vai dar

∫ 0 L d z z r 2 + z 2 3 / 2   = - 1 r 2 + z 2 z = 0 z = L = 1 r -   1 r 2 + L 2

Ps: Essa integral provavelmente estará no seu formulário! Se não estiver, não se desespere! Para fazer, é só fazer a substituição u = z 2 + r 2 e depois ter d u = 2 z d z :)

Assim, a nossa força fica

F → f i o = λ Q 4 π ϵ 0 1 r -   1 r 2 + L 2 k ^

Passo 3

Agora temos trabalhar com esse disco vazado

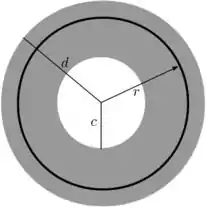
Esse disco vazado é constituído de anéis de raio r ( c < r < d ). Mas o enunciado já nos disse qual é o campo de um anel com carga Q e raio r . Então temos que tentar aproveitar essa informação para facilitar o nosso problema!

Sabemos que esse disco tem densidade superficial de carga σ , isso significa que

σ = d q d A d i s c o → d q = σ d A d i s c o

Em coordenadas polares (já que estamos falando de um disco!) essa área pode ser reescrita como r d r d θ

d q = σ r d r d θ

Se integrarmos essa expressão em θ , obteremos a carga total de um desses anéis de raio r que constituem o disco

d q a n e l = 2 π σ r d r

Aqui vou fazer uma observação interessante: o primeiro d q = σ r d r d θ é o quanto de carga tem em um infinitésimo de área d A enquanto que d q a n e l = 2 π σ r d r é o quanto de carga tem em um anel de raio r . Sacou a diferença?

Passo 4

Agora o campo de cada anel é dado por

d E → a n e l = 1 4 π ϵ 0 d q a n e l z r 2 + z 2 3 / 2   k ^

onde trocamos o Q por d q a n e l e agora o campo gerado por um anel é um diferencial. Dessa forma temos que o campo gerado por todo o disco vai ser

E → d i s c o = ∫ d E → a n e l

E → d i s c o = ∫ 1 4 π ϵ 0 d q a n e l z r 2 + z 2 3 / 2   k ^

E → d i s c o = 1 4 π ϵ 0 ∫ 2 π σ r d r z r 2 + z 2 3 / 2   k ^

E → d i s c o = σ z 2 ϵ 0 ∫ c d r d r r 2 + z 2 3 / 2   k ^

Essa integral em r é igual a que fizemos no item (a)!

E → d i s c o = σ z 2 ϵ 0 - 1 r 2 + z 2 r = c r = d k ^

E → d i s c o = σ z 2 ϵ 0 1 z 2 + c 2 - 1 z 2 + d 2 k ^

Resposta

  1. F → f i o = λ Q 4 π ϵ 0 1 r -   1 r 2 + L 2 k ^
  2. E → d i s c o = σ z 2 ϵ 0 1 z 2 + c 2 - 1 z 2 + d 2 k ^

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri