Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 7012345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686971727374757677787980818283848586

Enunciado

UFF. Física 2. P1. 2022.1. Questão 5.

5ª questão - Uma carga de 2,0   n C está distribuída uniformemente em um segmento do eixo x que vai de x = 0 a x = 3   m . Qual é a componente x do campo elétrico no ponto sobre o eixo y localizado em y = 2   m ?

A) - 1,3   N / C

B) - 2,4   N / C

C) - 4,0   N / C

D) - 5,7   N / C

E) - 9,0   N / C

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão temos um fio carregado que está localizado no eixo x , mais exatamente entre x = 0   m e x = 3   m .

A carga contida no fio é de 2,0   n C e queremos saber qual é a componente x do campo elétrico em um ponto sob o eixo y em y = 2   m .

E então! Como podemos obter esse resultado? 🤔🤔

Primeiro de tudo, vamos analisar como é a distribuição do nosso fio no plano cartesiano.

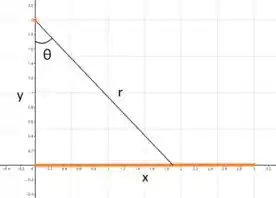
Em uma linha de carga como no nosso caso, separamos cada pedaço infinitesimal d q para analisar como esse pedaço contribui para o campo E .

Não podemos calcular capa pedaço infinitesimal pois isso resultaria em infinitas contas, então vamos usar uma formula que já conhecemos!

Bora ver qual é? 😁

Passo 2

Cada pedacinho d q se comporta como uma carga pontual, portanto a formula que descreve esses campos é dada como

E = k Q r 2 r ^

Aplicando o cálculo infinitesimal, temos

d E = k d Q r 2 r ^

Mas o que é r ?, perceba que um triangulo retângulo se forma entre x y r onde r é a hipotenusa, então podemos dizer que

r = x 2 + y 2

Substituindo em d E , temos

d E = k d Q x 2 + y 2 r ^

Estamos interessados no componente x do campo elétrico, ou seja, d E x

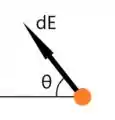
Você concorda que E x é dado pelo s e n θ de d E ? Ou seja

d E x = k d Q x 2 + y 2 s e n θ

Mas o que é s e n θ ? Cateto oposto sobre hipotenusa, correto?

s e n θ = x r = x x 2 + y 2

Substituindo em d E x

d E x = k d Q x 2 + y 2 x x 2 + y 2

Por fim, o que é d Q ?

Como nossa carga é linear, a densidade linear λ é dada por λ = d Q d L , logo d Q = λ d L

d E x = k λ d L x 2 + y 2 x x 2 + y 2

Entendeu até aqui? 👀

Passo 3

Agora vamos organizar nossa equação

d E x = k x λ d L x 2 + y 2 x 2 + y 2

d E x = k x λ d L x 2 + y 2 3 2

Perceba que d L é o infinitesimal do comprimento da linha de carga, ou seja, x

d E x = k x λ d x x 2 + y 2 3 2

Integrando dos dois lados, temos

∫ d E x = ∫ x 0 x f k x λ d x x 2 + y 2 3 2

E x = k λ ∫ 0 3 x x 2 + y 2 3 2 d x

Se aplicarmos o método de substituição u d u , fazendo x 2 + y 2 como u e consequentemente d u = 2 x d x ou x d x = d u / 2 , temos

∫ x x 2 + y 2 3 2 d x = ∫ 1 2 u 3 2 d u = ∫ u - 3 2 2 d u

Pelo método de integração polinomial, temos

∫ u - 3 2 2 d u = u - 3 2 + 1 2 - 3 2 + 1 = u - 1 2 2 - 1 2

Simplificando o resultado

∫ 1 2 u 3 2 d u = - 1 u

Substituindo u por x 2 + y 2 de volta

∫ x x 2 + y 2 3 2 d x = - 1 x 2 + y 2

Aplicando os limites de integração, vamos obter

∫ 0 3 x x 2 + y 2 3 2 d x = - 1 3 2 + y 2 - - 1 0 2 + y 2

∫ 0 3 x x 2 + y 2 3 2 d x = 1 y 2 - 1 9 + y 2 = 1 y - 1 9 + y 2

Bacana, não é? 😁

Passo 4

Até agora, nosso E x é dado por

E x = k λ 1 y - 1 9 + y 2

Resta apenas definirmos k , λ e y .

k é a constante eletrostática dada por 8,99 · 10 9 N m 2 C 2 , λ é dada por d Q d L , ou seja, a carga sobre o comprimento em linhas de cargas uniformes, logo

λ = 2,0 3 n C = 2 3 10 - 9 C

Por fim, y é a altura que nosso ponto se encontra no plano cartesiano, ou seja, y = 2

Aplicando essas substituições

E x = 8,99 · 10 9 2 3 10 - 9 1 2 - 1 9 + 2 2

E x = 1,3   N / C

Sabemos que pela imagem abaixo, a componente E x é voltada para o lado negativo de x

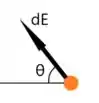
Logo, o que encontramos na verdade é o modulo de E x , portanto

E x = - 1,3   N / C

É isso! Nossa resposta condiz com a alternativa A)!

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

A) - 1,3   N / C

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri