Quatro fios finos de mesmo comprimento estão dispostos no plano simetricamente em torno da origem, como mostrado na figura abaixo. Cada um dos fios dispostos ao longo do eixo possui uma carga , estacionária e uniformemente distribuída. Já os fios dispostos ao longo do eixo possuem, cada um, uma carga , também estacionária a uniformemente distribuída.

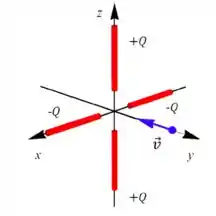
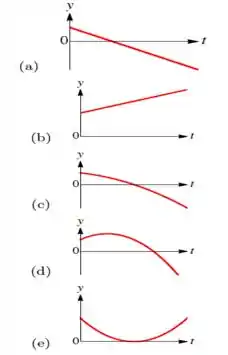
No instante de tempo , uma partícula de carga encontra-se sobre o eixo , deslocando-se com velocidade  . Dentre os gráficos abaixo, qual deles descreve o movimento subsequente da partícula?

Para entendermos o que está acontecendo na situação dada pelo problema, vamos considerar sua análise em duas partes separadas, como mostra a figura abaixo. Analisamos primeiro como é o campo elétrico resultante sobre a carga no plano e depois sobre o plano .

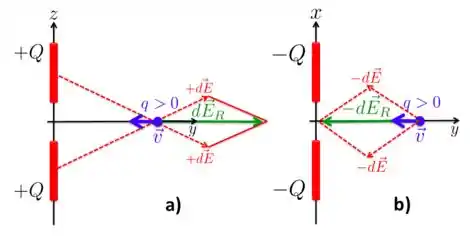
No plano , caso mostrado figura a) acima, cada elemento de carga de uma barra em terá um elemento idêntico e simétrico na outra barra que está em . Como ambos elementos são positivos, eles produzirão um campo de afastamento de mesma intensidade na posição da carga , como está representado na figura ).

Veja que na direção do eixo , as componentes do campo terão mesmo módulo, mesma direção, porém sentidos contrários. Isso significa que esse campo terá apenas componente na direção e o campo elétrico resultante é .

No plano , os campos são de aproximação, já que cada elemento de carga das barras em é negativo. Da mesma maneira que no plano , as componentes do campo na direção se cancelam e só há componente do campo na posição da carga na direção . O campo elétrico resultante nesse caso é e tem mesmo módulo que .