Considere um segmento retilíneo, de comprimento , disposto sobre o eixo como mostra a figura abaixo. Ele encontra-se carregado com um densidade linear de carga constante .
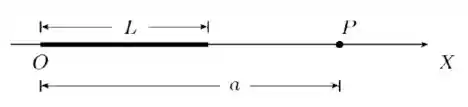
- Determine o campo elétrico (módulo, direção e sentido) em um ponto sobre o eixo , localizado a uma distância da extremidade do segmento que está sobre a origem .
- Uma partícula de carga é posicionada sobre o ponto . Determine a força elétrica (módulo, direção e sentido) que essa partícula exerce o segmento.
- Determine uma expressão assintótica para a força encontrada no item anterior no limite de . Interprete esse resultado.
Passo 1
a) A primeira coisa que precisamos fazer aqui é olhar apenas para um elemento de comprimento do segmento, de largura infinitesimal , localizado a uma distância de , conforme está na figura abaixo. Esse elemento está à uma distância do ponto onde queremos calcular o campo elétrico.
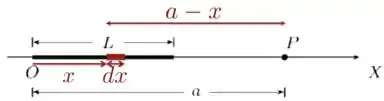
Este elemento possui uma carga e produz um campo elétrico em que é dado por:
Para encontrar o campo elétrico total, precisamos integrar sobre todo o comprimento do segmento:
Resolvendo a integral, temos
Assim o campo fica
sendo . Repara que, se a carga do segmento é positiva, , vai apontar na direção e sentido de ; se , estará ao longo de .
Passo 2
b) Vimos que a força eletrostática é uma força que obedece a terceira lei de Newton. Portanto, a força atuando na carga devida ao segmento carregado de comprimento tem o mesmo módulo, mesma direção, porém o sentido contrário da força que atua no segmento de comprimento devida à carga :
Isso significa que para encontrarmos a força que a carga produz no segmento, basta encontrarmos a força que o segmento exerce sobre a carga em e invertermos seu sinal. Como já encontramos o campo que o segmento produz em , que é onde vai ser colocada, a força que sente é:
o que vai nos dar que a força no segmento fica assim:
Passo 3
c) Se tomamos o limte de , vamos ver que , o que vai dar para a gente que a força que atua sobre o segmento é:
onde é a carga total do segmento.
Vemos que o resultado acima corresponde à força coulombiana entre duas partículas puntiformes carregadas de cargas e , separadas por um distância . Este resultado é esperado, pois nesse limite o comprimento do segmento é desprezível quando comparado com a separação entre o segmento e a carga . Assim, como o segmento possui carga diferente de zero, ele também pode ser pensado como uma partícula pontual carregada quando se tem .