Uma barra isolante fina de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela encontra-se carregada de forma que a porção possui uma densidade linear de carga constante e a porção possui uma densidade linear constante . Considere os pontos e indicados na figura. Podemos afirmar que o campo elétrico produzido pela barra nestes pontos aponta, respectivamente, no sentido dos vetores:
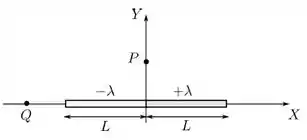
a) e
b) e
c) e
d) e
e) e
f) e
g) e
h) e
Passo 1
Esse probleminha é questão de apenas analisarmos o campo elétrico em cada um dos pontos. Pra isso, vamos lembrar um macete: quando a densidade de carga é positiva, o campo aponta em direção ao ponto; quando a densidade é negativa, o campo aponta em direção ao elemento de carga da barra. Vamos ver isso nos próximos passos :P
Passo 2
Vamos começar analisando o campo elétrico no ponto ok? Pra isso, vamos escolher um elemento de carga em e outro em . Ah, lembrando que esses elementos vão ser simétricos, vão estar na mesma distância do ponto .
Se chamarmos o campo elétrico da parte direita da barra de e o campo elétrico da parte esquerda de , o campo elétrico gerado por cada um desses elementos de carga vai ser assim
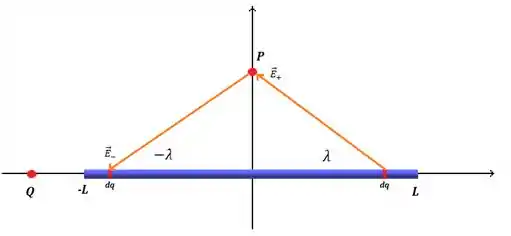
Ta, vamos separar esses dois vetores de campo elétrico em componentes e ? Vai ser esses vetores verdes da figura abaixo
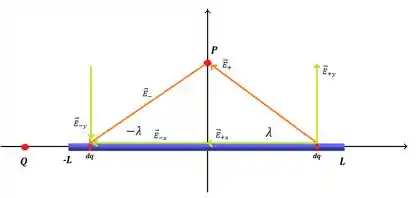
Cara, reparou que as componentes em se anulam? Porque elas possuem o mesmo módulo mas uma ta pra cima e a outra pra baixo.
Ao mesmo tempo, as componentes em se somam: as duas estão pra esquerda.
Logo, a gente conclui que o campo elétrico resultante no ponto vai ser a soma das componentes em , ou seja, vai estar pra esquerda, na direção .
Passo 3
Agora vamos ver como é o campo elétrico no ponto ?
Tanto para a parte positiva da barra quanto para a negativa, ele só vai ter componentes horizontais, assim
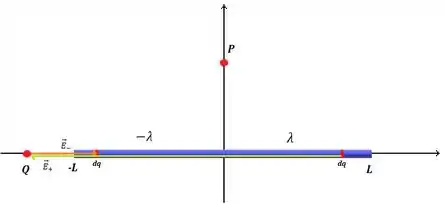
Agora vem uma coisa muito importante: olhando a imagem, a gente acha que o campo elétrico vai ser pra esquerda, já que o vetor é muito maior. Masss não, nesse caso, os elementos não estão à mesma distância do ponto , o elemento da parte negativa está muuito mais perto concorda? Então o campo elétrico na parte esquerda da barra vai ser bem mais forte do que na parte direita.
A parte esquerda então vai ter prioridade e portanto, o campo elétrico vai ser maior. Logo, o campo elétrico no ponto vai apontar pra direita, na direção .
Então, a nossa alternativa correta é a letra A :)
Resposta
a) e