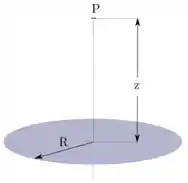
a) Um anel isolante, delgado de raio , possui uma distribuição uniforme de carga positiva . Calcule o vetor campo elétrico num ponto situado no eixo, a uma distância do plano anel.
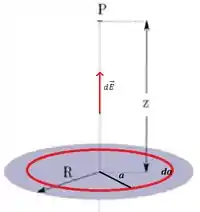
b) Um disco isolante de raio tem uma densidade superficial de carga positiva variável , onde é uma constante positiva e a distância radial medida desde o centro do disco. Calcule o vetor campo elétrico no ponto do eixo do disco à uma distância do seu plano (ver figura abaixo).
Passo 1
a) Ok, nesse problema temos um sistema de acordo com o que mostra a figura a seguir. Repare que foram desenhados dois vetores de campo elétrico pra conseguirmos enxergar como ele se comporta no eixo . Repare que haverá um vetor desse saindo de cada ponto infinitesimal do anel indo em direção ao eixo.
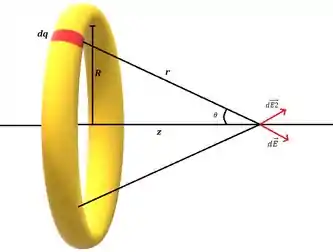
Vamos escolher um ponto infinitesimal qualquer do anel de carga e usar a expressão a seguir para calcular o seu campo elétrico no eixo .
Temos que calcular o campo elétrico em sua componente radial (vertical) e axial (horizontal). Masss, repare que as componentes radiais do campo elétrico do anel se cancelam aos pares, por exemplo na figura, a componente vertical de se anula com a componente vertical de , enquanto suas componentes horizontais se somam pois estão no mesmo sentido.
Logo, só teremos componentes axiais.
Passo 2
Então bora calcular a componente (axial) do campo elétrico
Agora vamos integrar para obter o campo elétrico
Usando pitágoras na figura, temos que
Passo 3
b) Nesse caso, a gente pode tratar o disco como se fosse um conjunto de vários anéis concêntricos. Vamos ilustrar o campo elétrico devido a um anel de carga , raio e largura .
No item A, a gente calculou que o campo elétrico devido a um anel carregado é
Então, para o anel da figura temos que
Integrando ambos os lados, temos que
Dessa vez, a integral de não vai ser pois temos uma densidade superficial de carga.
Podemos trocar a variável de integração de para sabendo que
Então:
Como :