A figura abaixo mostra dois anéis não condutores paralelos, com os centros sobre a mesma reta perpendicular aos planos dos anéis. O anel , de raio , possui uma carga uniforme ; O anel , também de raio , possui uma carga uniforme ; Os anéis estão separados por uma distância . O campo elétrico no ponto situado na reta que passa pelos centros dos anéis a uma distância do anel é zero. Determine a razão .
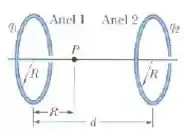
Passo 1
Primeiramente, vamos pensar em pedacinhos de carga opostos no anel e no campo elétrico que eles causam em um ponto no eixo do anel:
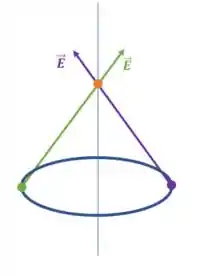
Esses pedacinhos de carga representados pelos pontos verde e roxo no anel geram dois vetores de campo elétrico. Vamos olhar esses dois vetores mais de perto:
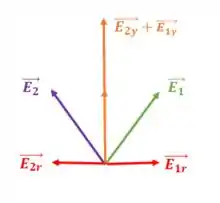
Você percebe comigo que decompondo esses vetores na direção do raio do anel , eles terão o mesmo módulo e direções opostas, ou seja, se cancelam. Enquanto as componentes na direção da reta do ponto , como temos vetores na mesma direção, teremos a soma de seus módulos.
Dessa forma pela simetria do problema, que o campo elétrico resultante se encontra sobre o eixo que liga os centros dos dois anéis, que chamaremos de . Assim:
Passo 2
O campo resultante em deverá ser zero. Como cada um está de um lado diferente do ponto , a diferença entre os campos deverá ser nula:
Passo 3
A nossa estratégia aqui vai ser a seguinte: vamos começar calculando a contribuição infinitesimal de cada pedacinho dos anéis, em cada anel, na determinação do campo elétrico total. Começando pelo primeiro anel:
A distâncias é a distância de um ponto qualquer do primeiro anel ao ponto . Como podemos ver na figura abaixo:
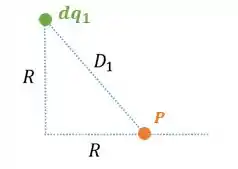
Por ser um triângulo retângulo, sabemos que a distância é igual a:
Passo 4
Pela mesma figura, podemos projetar cada o campo no eixo de simetria , para encontrar :
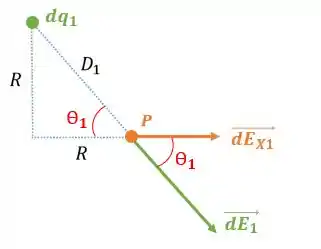
Como sabemos que :
Substituindo :
Para encontrar o módulo do campo , vamos integrar:
Pronto, um campo elétrico já foi! Vamos repetir o processo para o outro anel!
Passo 5
Cada pedacinho infinitesimal de carga do anel 2 irá gerar uma parcela do campo elétrico no ponto igual a :
Onde é a distância entre o ponto e essa carga infinitesimal do anel:
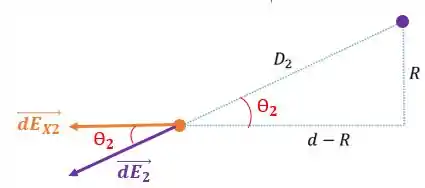
Como :
Passo 6
Pela mesma figura, podemos projetar cada o campo no eixo de simetria .
Percebemos que é igual a:
Substituindo e
Como , o módulo do campo :
Boa! Agora só temos que integrar o campo infinitesimal encontrado:
Passo 7
Pra fechar, basta igualar esses dois campos, conforme concluímos lá no Passo 2.
Cortando a constante e o raio :