Um anel isolante delgado de raio com densidade linear de carga uniforme encontra-se no plano . O eixo passa pelo centro do anel, coincidente com a origem dos eixos (Figura 1).
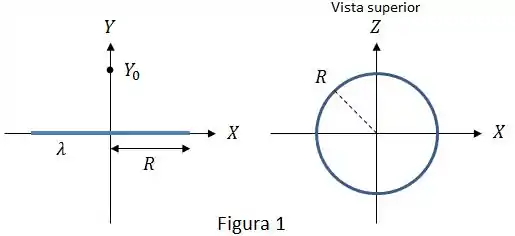
Calcule o vetor campo elétrico (módulo, direção e sentido) gerado pelo anel delgado num ponto qualquer sobre do eixo . Chame de a coordenada deste ponto ao longo do eixo Y.
Considere agora que o anel delgado é substituído por uma calha cilíndrica com base circular de raio , altura e densidade superficial de carga não uniforme. Como indicado na Figura 2, o plano corta a calha no plano mediano dela.
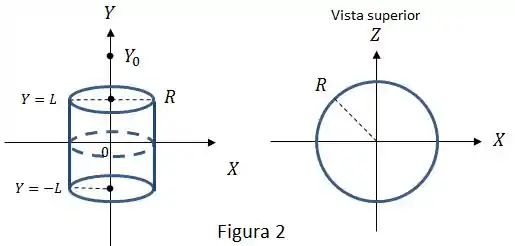
A partir do resultado do item calcule o campo elétrico (módulo, direção e sentido) gerado pela calha no ponto , considerando .
(Deixe o resultado em função dos símbolos das grandezas e parâmetros físicos)
Passo 1
Calcule o vetor campo elétrico (módulo, direção e sentido) gerado pelo anel delgado num ponto qualquer sobre do eixo . Chame de a coordenada deste ponto ao longo do eixo Y.
O primeiro passo aqui é escrever a expressão do campo elétrico gerado por um pedaço infinitesimal do arco, de carga :
Graficamente, a ideia é essa:
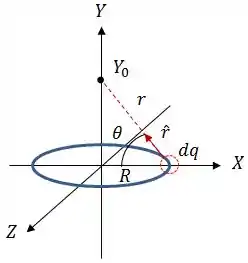
Daqui podemos tirar que:
Antes de continuarmos, aqui tem um detalhe aqui que é bem importante... vamos pegar dois pontos simétricos do anel pra ver o que acontece com o campo elétrico gerado por cada ponto de carga no ponto .
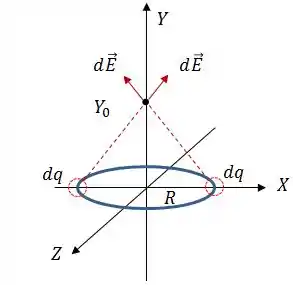
Consegue ver que as componentes horizontais vão se cancelar e as componentes verticais vão se somar? Isso acontece para cada par de pontos simétricos. O resultado disso é que o campo elétrico resultante vai estar somente sobre o eixo .
Assim, podemos nos preocupar em calcular somente a componente do campo elétrico.
Logo:
De acordo com a primeira figura, podemos dizer que:
Substituindo , e na expressão de , teremos:
Passo 2
Pra terminar, temos apenas que integrar esse cara entre e .
Finalmente:
Passo 3
A partir do resultado do item calcule o campo elétrico (módulo, direção e sentido) gerado pela calha no ponto , considerando .
No item anterior nós pegamos um pedaço infinitesimal do anel, com carga para calcular o campo elétrico gerado por todo o anel, certo?
Encontramos o seguinte resultado:
Uma coisa que podemos fazer aqui é dizer que toda a carga do anel será , logo:
Até aí, tudo bem.
O que faremos aqui é usar a mesma ideia de antes. Mas como agora se trata de uma calha, vamos dividi-la em vários anéis de carga , onde o campo elétrico gerado por cada anel no ponto vale:
Onde a carga está associada com a densidade superficial de carga por: .
Logo:
Pra terminar, basta integrar esse cara entre os limites de , que são e .
Finalmente:
Po, beleza... mas a resposta é essa daí mesmo?
Boa pergunta! Sim, a resposta é essa porque o problema disse que a casca tinha uma distribuição superficial de carga não uniforme , então já que não sabemos como esse cara se comporta, temos que deixá-lo dessa forma mesmo.
Resposta