UFRJ – Física 3 2020.2 – P1 – Questão 13
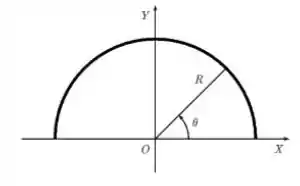
Um anel semicircular fino, isolante, de raio está posicionado sobre a porção superior do plano de um sistema de coordenadas e centrado na origem, como mostra a figura. Ele possui uma densidade linear de carga não uniforme dada por , sobre as componentes e do campo elétrico produzido pelo anel em seu centro, e , podemos afirmar que:
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
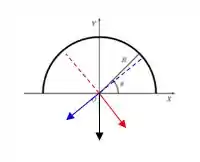Aqui temos que analisar a simetria. Como a carga é positiva, o campo produzido por cada pedacinho do anel está indicado ali na figura abaixo:
Aí as componentes horizontais se anulam e as componentes verticais se somam.
Passo 2
Em relação às componentes temos:
Beleza?
E analisando as alternativas, a correta é a (e).
Espero ter ajudado!
Resposta
Exercícios de Livros Relacionados
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri