Duas hastes plásticas, carregadas uniformemente com cargas e formam um anel de
raio como mostra a figura abaixo. A intensidade, direção e sentido do campo elétrico no centro do anel (ponto C) é:
- , horizontal apontando para esquerda
- , horizontal apontando para direita
- , horizontal apontando para esquerda
- , horizontal apontando para esquerda
Passo 1
Por simetria o campo gerado pela haste da esquerda é horizontal e aponta para direita. De forma parecida o campo gerado pela haste da direita é horizontal e aponta para direita também.
Como a diferença entre os dois anéis é somente o sinal da carga temos que
Passo 2
O campo horizontal gerado pelo anel da esquerda é dado por
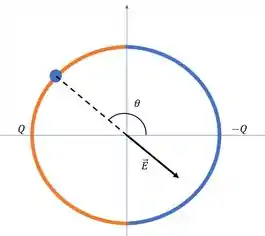
Passo 3
O infinitésimo de carga é dado por
E a densidade linear de carga é dada por
Assim
Passo 4
E o campo elétrico é dado por
Assim o campo total é dado por
Resposta
(B)
Exercícios de Livros Relacionados
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri