UFRJ – Física 3 2020.2 – P1 – Questão 6
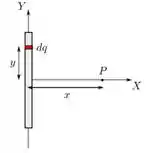
Uma barra fina, de comprimento , é posicionada ao longo do eixo de um sistema de coordenadas com seu centro sobre a origem, como mostra a figura abaixo. A barra está uniformemente carregada e possui carga total . Considere um elemento de carga infinitesimal da barra localizado no ponto como mostra a figura. Este elemento ocupa uma porção de comprimento infinitesimal da barra. Considere ainda o ponto localizado sobre o eixo . Qual é a expressão da componente vertical do campo elétrico infinitesimal produzido por no ponto ?
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Vou começar calculando a distância do ponto ao diferencial de carga :
E por simetria, temos que a resultante do campo elétrico vai ser proporcional ao cosseno do ângulo do campo com o eixo . E pelo desenho temos que o cosseno é:
Passo 2
O próximo passo é determinar o diferencial de carga. Como temos uma distribuição uniforme:
Passo 3
E agora vou juntar tudo isso:
Resgatando os resultados dos passos anteriores temos:
Beleza?
E analisando as alternativas, a correta é a (c).
Espero ter ajudado!