Campo Elétrico, Densidade de Carga, Campos Elétricos e Corpos Carregados
Na figura abaixo duas barras isolantes muito finas, ambas de comprimento , estão uniformemente carregadas. Uma das barras possui carga e a outra barra possui carga desconhecida. As barras estão posicionadas em direções perpendiculares, conforme a figura.
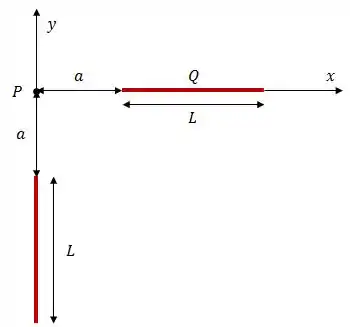
Determine o vetor campo elétrico (módulo, direção e sentido) no ponto produzido pela barra de carga ;
Sabendo que ao colocar uma partícula carregada positivamente em , a força exercida sobre esta faz um ângulo de com o eixo , calcule a componente do campo elétrico total;
Determine a densidade linear de carga da barra cuja carga é desconhecida;
Passo 1
Determine o vetor campo elétrico (módulo, direção e sentido) no ponto produzido pela barra de carga ;
O primeiro passo é escrever a expressão do campo elétrico gerado por uma carga infinitesimal , dado por:
Graficamente, a ideia é essa:
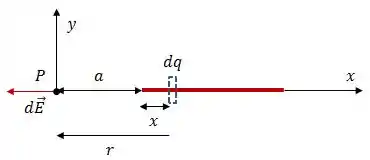
Onde:
Fazendo essas alterações:
Passo 2
Pra finalizar, temos apenas que integrar esse cara entre e :
Finalmente:
Passo 3
Sabendo que ao colocar uma partícula carregada positivamente em , a força exercida sobre esta faz um ângulo de com o eixo , calcule a componente do campo elétrico total;
Como a partícula colocada no ponto está carregada positivamente, a força elétrica resultante necessariamente vai apontar na mesma direção e sentido do campo elétrico resultante. Isso significa que o campo elétrico resultante fará um ângulo de com o eixo .
Além disso, o campo elétrico resultante será a soma vetorial dos campos elétricos das barras horizontal (que calculamos na letra ) e vertical (que é o que queremos calcular).
Graficamente, o que acontece é o seguinte:
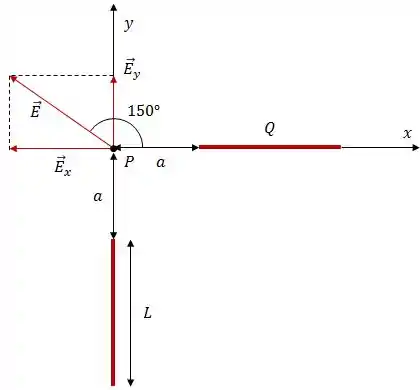
Olhando somente para os vetores:
Assim, podemos dizer que:
Finalmente:
Passo 4
Determine a densidade linear de carga da barra cuja carga é desconhecida;
Bom, a barra vertical tem o mesmo comprimento , e a densidade de carga linear é dada por:
Então o nosso trabalho aqui é calcular a carga da barra vertical.
O campo elétrico gerado por essa barra, no ponto , vai ter a mesma cara do campo elétrico gerado pela barra horizontal, a única diferença é que chamaremos a carga da barra vertical de , logo:
Simplificando esses caras, teremos:
Portanto:
Resposta