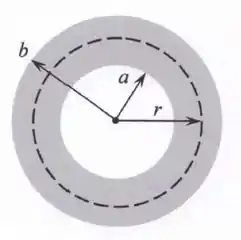
A figura ao lado ilustra uma esfera oca não-condutora de raio interno e raio externo que tem densidade volumétrica de carga variável para , onde é uma constante positiva e denota a distância radial ao centro da esfera. Tal esfera está localizada no vácuo, cuja constante de permissividade elétrica é dada por . Nestas condições, calcule:
- A carga elétrica total da esfera oca.
- O módulo do campo elétrico para .
- O módulo do campo elétrico para .
- O módulo do campo elétrico para .
Passo 1
a) Para encontrarmos a carga elétrica total contida na esfera oca, temos que fazer a seguinte integral:
em que está fora da integral porque é constante.
Agora, a gente precisa escrever corretamente o elemento infinitesimal de volume . Para isso, devemos imaginar uma casca esférica de largura e raio . O elemento de volume correspondente é obtido multiplicando a área da esfera de raio pela largura :
Substituindo isso na expressão para a carga total e resolvendo a integral, teremos:
Passo 2
b) Vamos imaginar uma gaussiana esférica de raio concêntrica à casca esférica. Nesse caso, nossa gaussiana engloba toda a carga , cuja expressão já encontramos. Por isso, o lado direito da lei de Gauss já temos. Basta trabalharmos o lado esquerdo agora.
Como a distribuição de cargas é uma função apenas de , que é a distância radial até o centro da esfera, então o campo elétrico que as cargas produzem tem simetria esférica e, por isso, esse campo depende apenas da distância até o centro da esfera e o vetor correspondente aponta na direção de :
O campo campo está apontando para fora da gaussiana, já que a carga da esfera é positiva, e ele tem o mesmo valor em todos os pontos à mesma distância do centro.
Além disso, como sempre, devemos colocar o elemento de área apontando para fora da gaussiana, ou seja, , e com isso os vetores e são paralelos. Se jogamos tudo isso junto no lado esquerdo da lei de Gauss, vamos ter o seguinte:
Dessa expressão, a gente tira que o módulo do campo elétrico em é:
Passo 3
c) Para resolver este item, precisamos considerar uma gaussiana esférica dentro da região e depois fazemos os mesmos argumentos do Passo 2 para encontrar o lado esquerdo da lei de Gauss, que é: .
O lado direito, que depende da carga total dentro da região , é obtido apenas mudando o limite superior da integral que fizemos no Passo 1: trocamos por .
Fazendo isso, vamos ter o seguinte:
Passo 4
d) Para esse caso, de novo fazemos uma gaussiana esférica de raio concêntrica à esfera. Nesse caso, como não há carga nessa região: