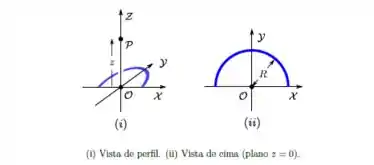
Um fio semicircular fino, de raio R, encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva λ.

(a) Determine a carga total do fio.

(b) Qual(is) componente(s) do vetor campo elétrico resultante em um ponto qualquer do eixo Z é(são) nula(s)? Justifique.

(c) Deduza, em detalhe, uma expressão para o vetor campo elétrico resultante no ponto P acima mencionado.

B)

Bom, a componente em x deve ser nula, pois é neste eixo que temos dois elementos simétricos em relação a origem. E cada um deles vai gerar um campo na direção oposta ao do outro. Com isso, o campo resultante nessa direção será nulo.

c)Vamos fazer um desenho pra ajudar.

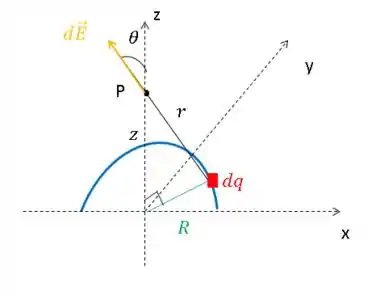
Pelo item b, já vimos que a componente em x é nula. Então só temos que calcular as componentes y e z.

Primeiro em z.

Mas . E considerando o triângulo retângulo formado. Temos que . Então

Podemos usar o teorema de Pitágoras e

Integrando isso temos:

Na segunda igualdade usei o resultado do item a.

De novo, pelo item a:

Show! Vamos para a componente y.

Vimos que . Agora, a componente no plano xy do campo magnético é Para termos a componente na direção y temos que projetar na direção desse eixo, então ficamos com . Esse menos é porque o aponta para o sentido negativo do eixo.

A vista do plano xy é assim:

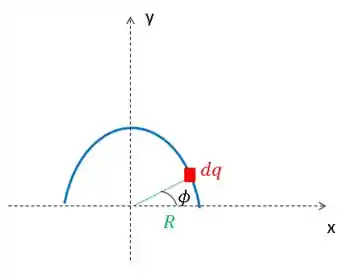
Show. Vamos lá.

Mas . E considerando o triângulo retângulo formado na figura lá de cima. Temos que . Então

Substituindo o :

Substituindo :

Para deixarmos em termos da carga total Q:

Show! Então o vetor campo elétrico no ponto P é