A estrutura ilustrada na figura abaixo é composta por três barras isolantes, uma semicircular de raio , e duas retilíneas e que são perpendiculares entre si. As três barras apresentam uma densidade linear de carga constante e positiva . O ponto é o centro do semicírculo e a origem do sistema de coordenadas -.
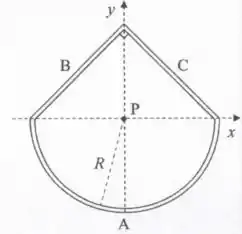
- Calcule o vetor campo elétrico produzido apenas pela barra semicircular no ponto .
- Calcule o vetor campo elétrico produzido por ambas as barras retilíneas e , no ponto .
- Se colocamos uma carga pontual negativa no ponto , em que direção e sentido esta carga vai se mover? Explique sua resposta.
Dado:
Passo 1
a) Para a barra semicircular , como mostra a figura abaixo, vemos que o campo elétrico resultante estará ao longo da direção . As componentes ao longo do eixo se cancelam aos pares, já que a distribuição de cargas é uniforme. Por isso, o campo resultante é:
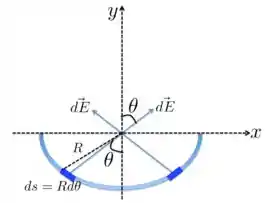
Como o elemento infinitesimal de carga é e a distância entre o elemento , que tem carga , é , podemos escrever o módulo como:
Do jeito que a gente desenhou o ângulo , ele varia de (quando o elemento de carga tá na ponta esquerda) até (quando o elemento de carga tá na ponta direita). Assim:
Isso nos conduz a
Portanto, o vetor campo elétrico produzido pela barra semicircular é
Passo 2
b) A primeira coisa que precisamos notar é que o comprimento de cada barra é . Isso a gente obtém aplicado o teorema de Pitágoras no triângulo da figura à esquerda abaixo. Além disso, o módulo do campo elétrico que essas barras carregadas produzem na origem tem o mesmo valor: , já que cada barra está disposta da mesma maneira e possui a mesma densidade de cargas . Para continuarmos, veja bem as quantidades que estão representadas na figura abaixo.
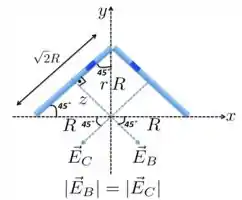
Antes de escrevermos os vetores para esses campos, vamos encontrar o valor de seus módulos. Como e (veja a figura acima), temos que
em que integramos sobre todo o comprimento da barra.
Como o integrando é uma função par na variável , podemos escrever que
em que já utilizamos o resultado da integral dado no enunciado e aplicamos os limites.
Agora, para fechar, da figura, vemos que , o que resulta em . Substituindo isso na expressão acima, teremos que
Como mostra a figura, os vetores e podem ser decompostos nas direções e e esses vetores formam um ângulo de com o eixo . Fazendo isso, obtemos que
O campo resultante no ponto será a soma vetorial desses dois campos. Portanto,
que confirma que o campo devido às barras tem direção e sentido do eixo .
Passo 3
c) Uma carga negativa colocada no ponto , estará sob a ação do campo resultante , que é a soma vetorial do campo da barra semicircular e do campo das duas barras retilíneas e . Logo, a força sobre a carga será:
Utilizando os resultados que obtivemos nos itens a) e b), chegamos a
Portanto, a carga se move para cima, no sentido positivo do eixo .