UFRJ – Física 3 2020.2 – P1 – Questão 15
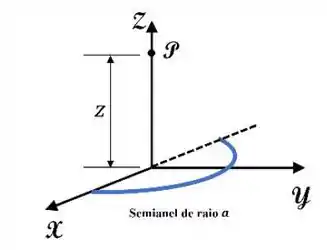
Um anel semicircular de raio está carregado negativamente com uma carga distribuída uniformemente ao longo do seu comprimento. Qual é o valor da componente do campo elétrico produzido pelo semianel em um ponto sobre o eixo , localizado a uma distância da origem?
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Aqui temos que a distância do semianel até o ponto não muda e vale .
Quando somamos toda carga obtemos , pois vamos somar todo comprimento do anel. Por simetria temos que a componente do campo é anulada. A componente é proporcionao ao cosseno do ângulo com o eixo . Então temos o seguinte:
Passo 2
O próximo passo é juntar tudo e obter a componente do campo (lembrando que é negativo pois a carga é menor que zero):
Beleza?
Espero ter ajudado!