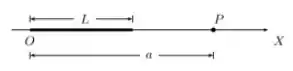
. Considere uma barra fina, retilínea e isolante, de comprimento , disposta sobre o eixo de um sistema de coordenadas com uma de suas extremidades sobre a origem, como mostra a figura abaixo. Ela encontra-se carregada com uma densidade linear de carga estacionária, mas não-uniforme dada por , onde é uma constante positiva.
Determine a carga total da barra.
Determine o vetor campo elétrico em um ponto sobre o eixo , localizado a uma distância da extremidade da barra que está sobre a origem .
Passo 1
Então galera, vamos acabar com esse problema!
Para determinar a carga total da barra temos que considerar um elemento de comprimento infinitesimal da barra dado por .
Fazemos isso porque como temos a densidade linear de carga podemos escrever um elemento de carga da barra como:
Com isso basta integrar em todo comprimento da barra teremos a carga total da barra.
Para encontrar o campo elétrico no ponto vamos considerar o mesmo elemento de carga e considerar que ele se encontra a uma distância do ponto .
Então o elemento de campo elétrico gerado por esse elemento de carga em é dado por:
Então para encontrar a contribuição de toda a barra sobre o ponto basta integrarmos essa expressão em todo o comprimento da barra.
Mãos à obra então!
Passo 2
Vamos começar com o item , temos:
Mas o enunciado nos diz que:
Então temos:
Assim a carga total é:
Então temos que:
Prontinho encontramos a carga a total!
Passo 3
Vamos agora encontrar o campo elétrico causado pela barra em , como vimos no passo a contribuição de um elemento de carga é:
Usando o fato de que
Temos que:
Agora temos que o campo causado por toda a barra é dado por:
Então temos:
Conseguimos encontrar o vetor campo elétrico em um ponto .