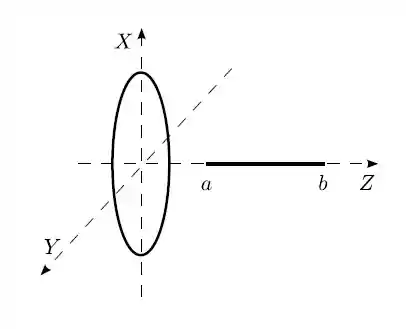
Um anel circular, muito fino, de raio , encontra-se em repouso no plano , com seu centro na origem. Tal anel possui carga total , uniformemente distribuída.

1. Calcule o vetor campo elétrico (módulo, direção e sentido) devido a tal anel num ponto do eixo , com cota arbitrária .
2. Considere agora um bastão retilíneo, muito fino, em repouso, situado no eixo , entre e . Tal bastão também possui carga total , uniformemente distribuída. Calcule o vetor força elétrica sobre tal bastão devido ao anel. (Sugestão: a força sobre o bastão constitui-se da soma vetorial das forças sobre cada elemento infinitesimal do bastão carregado).

Podemos utilizar argumentos de simetria para justificar que só existe componente em :

Continuando:

Encontramos a componente por decomposição:

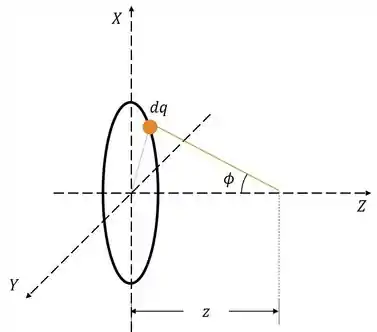
Lembrando que o triângulo é retângulo na origem dos eixos coordenados, e não onde está a carga .

Além disso, como a gente quer o campo no eixo , que é o eixo de simetria do anel, note como o campo não depende das coordenadas e . O anel está no plano , então podemos tirar da integral um tanto de coisas:

A integral da carga no anel dá a sua carga total:

Agora pra calcular a força é só montar a equação da força infinitesimal que o campo faz numa carga infinitesimal (Lei de Coulomb):

Integrando na barra toda:

Substituindo:

Agora atenção! Trocamos o diferencial de carga pela equação da densidade da barra:

Sabemos que a distribuição de carga é uniforme, portanto isto implica numa densidade constante igual à:

Que é a carga total pelo comprimento total. Logo:

Integrando:

Fazemos substituição simples:

A indefinida fica:

Logo:

Fica ligado de não esquecer esse sinal de menos na frente de tudo. E é só!