Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 6212345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061636465666768697071727374757677787980818283848586

Enunciado

Densidade de Carga, Campos Elétricos e Corpos Carregados

Considere uma barra retilínea, fina, disposta no eixo Z , entre as coordenadas z = - L e z = L L > 0 . Em tal barra, existe uma distribuição de carga, com densidade linear

λ z = A z

sendo A = c o n s t .

a Calcule a carga total da barra Q t o t .

b Determine o campo elétrico resultante (devido à barra) em um ponto do seu plano médio, a uma distância s da barra.

c Determine a expressão assintótica de tal campo, no limite em que s ≫ L . Interprete o seu resultado.

Passo 1

a Calcule a carga total da barra Q t o t .

Por definição, a densidade linear de carga é dada por:

λ z = d q d z

d q = λ z d z

Daqui já podemos calcular a carga total da barra, basta integrar esse cara de - L ≤ z ≤ L .

Q t o t = ∫ - L L λ z d z

Onde λ z = A z .

Como se trata de uma função modular, podemos dizer que:

z = - z ,     p a r a - L ≤ z ≤ 0 z ,     p a r a   0 ≤ z ≤ L

Isso significa que teremos que dividir a nossa integral em duas partes: a primeira com o intervalo - L ≤ z ≤ 0 e a segunda com 0 ≤ z ≤ L .

Logo:

Q t o t = ∫ - L 0 λ z d z + ∫ 0 L λ z d z

Substituindo λ z , teremos:

Q t o t = ∫ - L 0 A - z d z + ∫ 0 L A z   d z

Q t o t = - A ∫ - L 0 z   d z + A ∫ 0 L z   d z

Q t o t = - A z 2 2 - L 0 + A z 2 2 0 L

Q t o t = - A 2 0 - L 2 + A 2 L 2 - 0

Q t o t = A L 2 2 + A L 2 2

Finalmente:

Q t o t = A L 2

Passo 2

b Determine o campo elétrico resultante (devido à barra) em um ponto do seu plano médio, a uma distância s da barra.

Vamos começar explorando a simetria do problema. Vamos pegar dois pontos simétricos, ambos de carga d q e analisar o campo elétrico resultante entre esses dois caras:

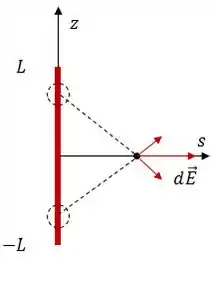
É possível ver que as componentes na direção z ^ irão se anular e só sobrará as componentes na direção radial s .

Isso vai acontecer pra qualquer par de pontos simétricos, ou seja, o campo elétrico resultante será do tipo:

E → = E s ^

Agora podemos seguir em frente.

Passo 3

Pra começar, vamos pegar um pedaço infinitesimal da barra, de carga d q , e escrever a expressão de um campo elétrico infinitesimal d E → gerado por ele em um ponto a uma distância s do ponto médio da barra.

d E → = 1 4 π ϵ 0 d q r 2 r ^

Graficamente, a ideia é essa:

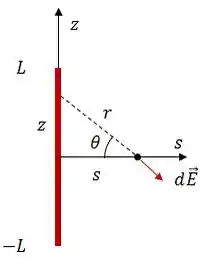
Daqui podemos tirar que:

d q = λ z d z

r = z 2 + s 2

r ^ = cos ⁡ θ s ^ - sen ⁡ θ z ^

r ^ = s z 2 + s 2 s ^ - z z 2 + s 2 z ^

Logo:

d E → = 1 4 π ϵ 0 λ z d z z 2 + s 2 3 / 2 s   s ^ + z   z ^

Mas como vimos anteriormente, E → = E s ^ . Então vamos nos preocupar somente com a componente na direção s ^ .

d E → = 1 4 π ϵ 0 s λ z d z z 2 + s 2 3 / 2 s ^

Passo 4

λ z = A z , logo:

d E → = s A 4 π ϵ 0 z d z z 2 + s 2 3 / 2 s ^

Agora basta integrar esse cara de – L até L .

E → = s A 4 π ϵ 0 ∫ - L L z d z z 2 + s 2 3 / 2 s ^

Novamente, vamos dividir essa integral em dois intervalos:

E → = s A 4 π ϵ 0 ∫ - L 0 - z d z z 2 + s 2 3 2 + ∫ 0 L z   d z z 2 + s 2 3 2 s ^

E → = s A 4 π ϵ 0 - ∫ - L 0 z   d z z 2 + s 2 3 2 + ∫ 0 L z   d z z 2 + s 2 3 2 s ^

Essa integral é resolvida através de uma substituição simples:

u = z 2 + s 2

d u = 2 z   d z → z   d z = d u 2

Logo:

E → = s A 4 π ϵ 0 - 1 2 ∫ u - 3 2 d u + 1 2 ∫ u - 3 2 d u s ^

E → = s A 4 π ϵ 0 1 u - 1 u s ^

Fazendo as substituições de volta, teremos:

E → = s A 4 π ϵ 0 1 z 2 + s 2 - L 0 - 1 z 2 + s 2 0 L s ^

E → = s A 4 π ϵ 0 1 s 2 - 1 L 2 + s 2 - 1 L 2 + s 2 - 1 s 2 s ^

E → = s A 4 π ϵ 0 1 s - 1 L 2 + s 2 + 1 s - 1 L 2 + s 2 s ^

E → = s A 4 π ϵ 0 2 1 s - 1 L 2 + s 2 s ^

Finalmente:

E → = s A 2 π ϵ 0 1 s - 1 L 2 + s 2 s ^

Passo 5

c Determine a expressão assintótica de tal campo, no limite em que s ≫ L . Interprete o seu resultado.

Ok, vamos começar reorganizando esse cara:

E → = s A 2 π ϵ 0 1 s - 1 L 2 + s 2 s ^

E → = A 2 π ϵ 0 s s - s L 2 + s 2 s ^

E → = A 2 π ϵ 0 1 - s L 2 + s 2 s ^

E → = A 2 π ϵ 0 1 - s L 2 s 2 + 1 s 2 s ^

E → = A 2 π ϵ 0 1 - 1 s s L 2 s 2 + 1 s ^

E → = A 2 π ϵ 0 1 - 1 L 2 s 2 + 1 s ^

Para L s → 0 , basta utilizar o binômio de Newton:

1 + x n ≈ 1 + n x + …

Ou seja,

1 L 2 s 2 + 1 = 1 + L 2 s 2 - 1 / 2 ≈ 1 + - 1 2 L 2 s 2 + …  

Logo:

E → ≈ A 2 π ϵ 0 1 - 1 - 1 2 L 2 s 2 + … s ^

E → ≈ A 2 π ϵ 0 1 2 L 2 s 2 s ^

E → ≈ A L 2 4 π ϵ 0 s 2 s ^

Lembrando que a carga total é Q t o t = A L 2

E → ≈ Q t o t 4 π ϵ 0 s 2 s ^

Repara só que esse é o campo gerado por uma carga pontual e faz sentido, né. Como a distância s é muito maior do que o comprimento da barra, é como se a barra fosse uma partícula e por isso o campo é o mesmo de uma partícula.

Eu sei que essa história de “binômio de Newton” deve ter fritado a sua cabeça, mas de vez em quando aparecem esses tipos de coisa nas provas... então é bom dar uma olhadinha nisso e em série de Taylor, só por via das dúvidas, beleza?

Resposta

a

Q t o t = A L 2

b

E → = s A 2 π ϵ 0 1 s - 1 L 2 + s 2 s ^

c

E → ≈ A L 2 4 π ϵ 0 s 2 s ^ = Q t o t 4 π ϵ 0 s 2 s ^

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri