Um anel circular fino e isolante de raio é posicionado sobre o plano de um sistema de coordenadas com seu centro na origem, como mostra a figura abaixo. Ele está carregado com uma densidade linear de carga estacionária, mas não uniforme dada por , onde é uma constante positiva e é o ângulo polar medido a partir do eixo positivo.
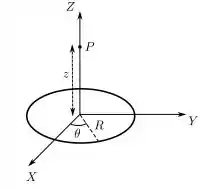
Sobre as componentes cartesianas , e do campo elétrico produzido pelo anel em um ponto sobre o eixo , é CORRETO afirmar que:
Passo 1
POW! É o seguinte, já vou te alertando que nesse item não vamos fazer nenhuma conta. Vamos apenas inspecionar a cara do campo elétrico nessa região beleza?
Cara... O problema nos disse que a densidade de carga no anel varia com o seno do ângulo ...
O é uma função que varia da seguinte maneira...
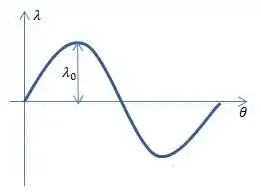
Isso significa que o ponto de maior carga em cima do disco é no ponto em cima do eixo e o ponto de menor carga (carga negativa) é no ...

Os pontos de carga é em cima do eixo , saca?
Então como vai ser o padrão do campo elétrico produzido por essas cargas no eixo ?
Passo 2
Ora, o ponto de maior carga positiva, produz um campo elétrico assim...
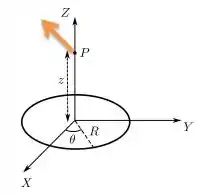
Já o ponto de carga negativa do lado oposto produz um campo elétrico assim...
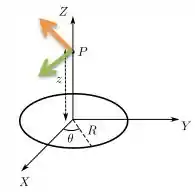
O resultado da soma desses dois campos elétricos é...
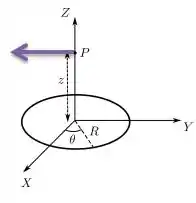
E olha que maneiro, devido à simetria de cargas nos demais pontos...

Todos os outros campos elétricos feitos pelas outras demais cargas são cancelados, sobrando apenas os campos feitos por esses dois extremos de cargas no eixo . Ou seja, o campo resultante no eixo é então apenas esse campo aqui...
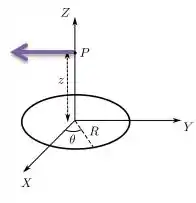
E esse campo resultante possui como componentes...
Resposta
Letra A.