Forças Elétricas, Campo Elétrico
Cinco cargas iguais a são igualmente espaçadas em uma semicircunferência de raio , conforme a figura.
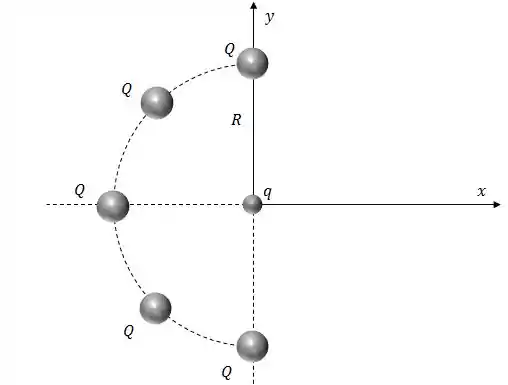
Determine a força (módulo, direção e sentido) que atua sobre uma carga localizada no centro da semicircunferência;
A partir do item , determine o vetor campo elétrico no centro da semicircunferência, considerando agora a carga como sendo uma carga de prova;
Passo 1
Determine a força (módulo, direção e sentido) que atua sobre uma carga localizada no centro da semicircunferência;
Bom, a força elétrica entre duas cargas é dada por:
Ou:
Pra começar, não é difícil ver que o problema apresenta uma certa simetria, concorda?
Então antes de começarmos a quebrar a cabeça com os cálculos, vamos tentar dar uma explorada nessa simetria porque pode acabar facilitando a nossa vida.
Vamos numerar as cargas pra facilitar a discussão aqui.
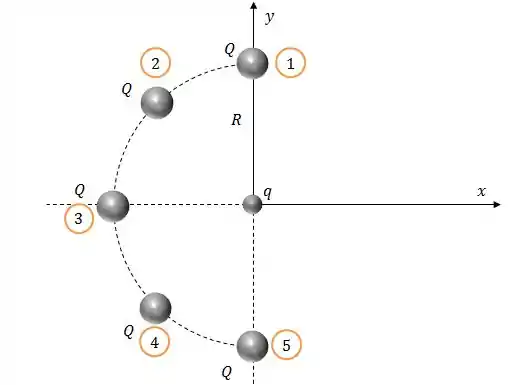
Fazendo um esboço das forças elétricas sobre a carga , podemos ver que tem como cancelar algumas coisas aqui.
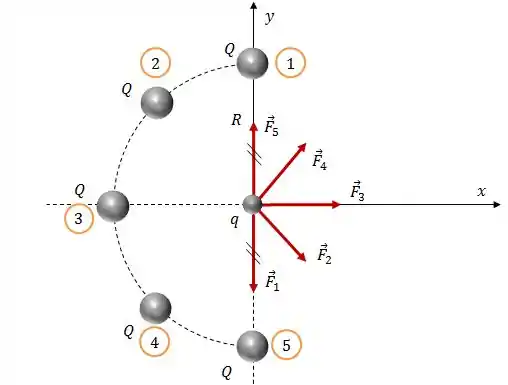
Como as cargas são iguais e as distâncias são as mesmas, as forças e possuem o mesmo módulo e direção, mas sentidos opostos, logo elas se cancelarão.
O mesmo vai acontecer com as componentes na direção das forças e . Justamente por conta da geometria do problema.
Isso significa que a força resultante estará na direção , somente.
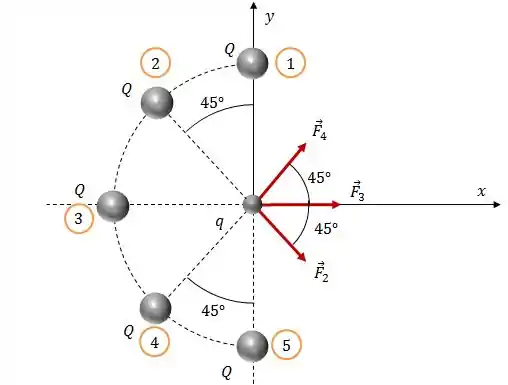
Portanto, a força resultante será:
Passo 2
Agora só precisamos calcular a força resultante.
Todas as forças possuem o mesmo módulo:
Portanto:
Passo 3
A partir do item , determine o vetor campo elétrico no centro da semicircunferência, considerando agora a carga como sendo uma carga de prova;
Por definição, o campo elétrico que atua sobre a carga de prova está relacionado com a força elétrica por:
Portanto:
Resposta