UFSCAR, Sem Campus, Física 3, AV1 - 2022.2 - Prof° Matheus Paes, Questão 1.
Questão 1 - Cinco cargas pontuais , , , , e são colocadas em sequência nos vértices de um pentágono de aresta . Qual o módulo do campo elétrico no centro deste pentágono?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, nosso objetivo é calcular o campo elétrico gerado por cargas pontuais dispostas nos vértices de um pentágono de de aresta.
As cargas pontuais possuem uma sequência de , , , , e .
Tem ideia do que temos que fazer? 🤔
A primeira coisa é descobrir a distância de cada vértice até o centro do pentágono.
A partir daí aplicamos a fórmula do campo elétrico para cada carga e no fim fazemos o somatório dos campos.
A fórmula campo elétrico gerado por uma carga é dado por
Em que e .
Entendeu? Bora começar! 😁
Passo 2
Vamos obter o valor da distância dos vértices até o centro. Pra isso, sabemos que um pentágono possui vértices. Se a distância de cada vértice ao centro do pentágono é , cada triângulo que é formado por dois raios e a aresta é dado por
Cortando um desses triângulos ao meio, formando dois triângulos retângulos temos que cada ângulo é dado por
Assim temos que se a aresta do pentágono é , então cada triangulo retângulo terá como cateto , veja só
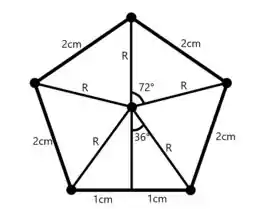
Se aplicarmos a lei do seno para esse triangulo retângulo, temos que
Isolando ...
Tranquilo até aqui? 😉
Passo 3
Agora, calculamos cada campo sabendo que o campo gerado por uma carga aponta para o mesmo sentido do raio .
Se , , , , e , então
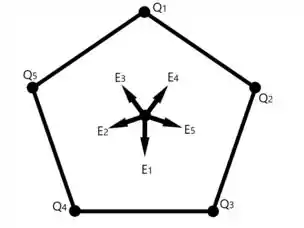
Bora lá!
Com o modulo dos campos obtidos, vamos obter os vetores resultantes das componentes nos eixos e .
Entendeu essa parte? 😎
Passo 4
Agora analisando os vetores dos campos, temos
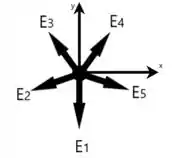
Para o eixo , temos que faz um ângulo de
Para , se o ângulo de a é e o ângulo entre e é , então
Para , podemos ver que o ângulo é , ou seja
Para , o ângulo entre ele e o eixo é , logo
E por fim, para , se faz com e de para tem , então
Logo, pela regra dos cossenos, o vetor resultante em é
Bacana, não é? 👀
Passo 5
Agora, para o eixo , vamos aplicar a lei dos senos com os ângulos que encontramos.
Assim, vamos obter o módulo do campo elétrico resultante obtendo o modulo dos vetores e .
Portanto, vimos que o modulo do campo elétrico resultante no centro do pentágono é ! Legal, né?
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
