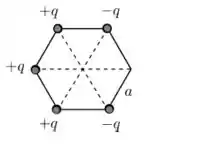
Cinco partículas carregadas são fixadas sobre os vértices de um hexágono regular de lado a como mostrado na figura abaixo. Os valores das cargas estão indicados na figura. Qual deve ser o valor da carga de uma sexta partícula a ser adicionada ao vértice desocupado de forma que o campo elétrico resultante produzido pelas seis partículas no centro do hexágono seja nulo?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Vamos pensar junto. O campo elétrico total no centro vai ser a soma vetorial dos campos elétricos de cada carga nessa posição. O campo elétrico de cargas pontuais aponta para “fora” se e para “dentro” se . Vamos marcar a direção e o sentido do campo de cada carga, no ponto central.

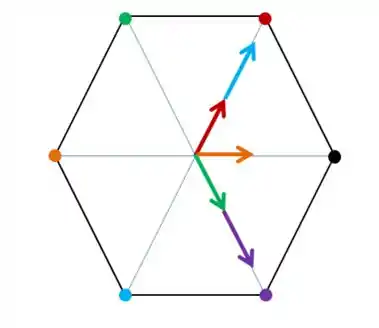
Fiz um esquema de cores. As setas azuis e roxas estariam embaixo da vermelha e da erde, eu só coloquei elas depois para conseguirmos ver, ok?

Agora, vamos pensar de uma forma esperta. O campo naquele ponto tem que zero. Na direção vertical o campo resultante é nulo. E o campo resultante tá na direção horizontal, para a direita. Com isso, já sabemos que o campo da carga preta deve apontar para a esquerda (para que tudo se anule), com isso, a carga no ponto preto deve ser positiva!

Já eliminamos metade das opções! Vamos encontrar o módulo dessa carga agora.

O campo elétrico de uma carga pontual é

Beleza, guarda isso aí.

O hexágono regular é dividido em seis triângulos equiláteros, aqueles ângulos internos tem . Com isso, o campo que tá na direção horizontal para a direita é

Porque temos 4 setas que fazem com a horizontal e o que está totalmente na horizontal.

Então

Show. Então a carga que está no ponto preto deve ter um campo tal que somado a esse dê zero. Então a carga lá é Q=. Como já vimos, a carga lá é positiva, então

Então o valor

Uhuul!