Originalmente, oito cargas puntiformes iguais ocupavam os vértices de um octógono regular, como mostrado na figura. Uma das cargas é removida.
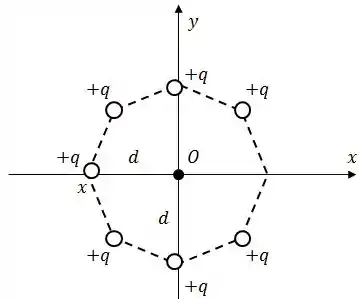
Qual é o módulo do campo elétrico no ponto , centro do octógono, depois da remoção da carga?
;
;
;
;
;
Passo 1
Vou te falar... a primeira vez que eu vi essa questão, eu pensei “Sério mesmo que eu vou ter que decompor e fazer a soma dos campos gerados por essas 7 cargas?!”.
Então, a verdade é que tem um jeito bem mais tranquilo de resolver a questão, vem comigo!
Pelo fato de se tratar de um octógono regular, se todos os vértices tivessem cargas com mesmo módulo e sinal, o campo no centro do octógono seria igual a zero!
Obs.: Isso aconteceria para qualquer polígono regular.
Passo 2
Então vamos colocar uma carga fictícia no vértice que está vazio e calcular o campo gerado por todas as outras 7 cargas.
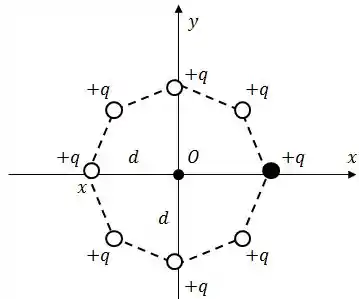
Fechando o octógono com a nossa carga fictícia, agora o campo elétrico no centro será igual a zero, logo:
Como estamos interessados no módulo do campo gerado pelas 7 cargas, este será igual ao campo gerado pela carga fictícia .
Logo, a resposta certa é a letra .
Resposta
;