Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Carga Pontual

Ver Teoria
Exercício 3112345678910111213141516171819202122232425262728293032333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192

Enunciado

UFRJ- Física 3 – PF 2018.2 - DIURNO - 1

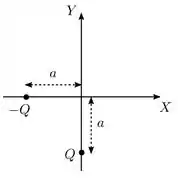
Duas partículas de cargas Q e - Q ( Q > 0 ) são fixadas sobre o plano X Y , como mostrado na figura abaixo (note que a > 0 ). Em que ponto deste plano deve ser posicionada uma terceira partícula, de carga 2 Q , para que o campo elétrico resultante produzido pelas três partículas seja nulo na origem?

  1. - a 2 , a 2
  2. a 2 , - a 2
  3. - a 2 , a 2
  4. a 2 , - a 2
  5. ( - a , a )
  6. ( a , - a )

Passo 1

Na origem a carga - Q produz o seguinte campo elétrico

E → - Q = - k Q a 2 x ^

Enquanto que a carga Q produz

E → Q = k Q a 2 y ^

Queremos colocar um carga 2 Q em algum lugar de tal forma que anule o campo total na origem. Chamando de E → 2 Q o campo produzido por essa carga então temos que

E → 2 Q + E → Q + E → - Q = 0

Substituindo o que a gente sabe

E → 2 Q + k Q a 2 y ^ - k Q a 2 x ^ = 0 → E → 2 Q = k Q a 2 x ^ - y ^

Passo 2

Como a carga é 2 Q , seria interessante fazer ela aparecer na nossa expressão. Pra isso vamos multiplicar e dividir por 2

E → 2 Q = k 2 Q a 2 x ^ - y ^ 2

E o módulo desse campo é

E → 2 Q = k 2 Q 2 a 2 1 2 + 1 2 = k 2 Q a 2

Beleza. Agora vamos desenhar esse campo.

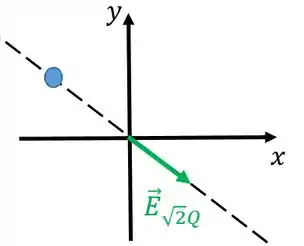
Ele tem o módulo das componentes x e y iguais. Isso indica que esse campo faz um ângulo de - 45 º com o eixo x .

Como a carga é positiva, o campo se afasta dessa carga, então a nossa carga está no segundo quadrante em cima da linha pontilhada. Pelo nosso desenho, vamos dizer que essa carga está na posição

( - b ,   b )

Assim a distância dela até a origem seria b 2 e o módulo do campo produzido por ela seria

E = k 2 Q 2 b 2 = k 2 Q 2 b 2

Comparando com o módulo do campo que sabemos o que é que tem que ser

k 2 Q 2 b 2 = k 2 Q a 2 → 1 2 b 2 = 1 a 2

a 2 = 2 b 2 → b = a 2

Assim finalmente achamos a posição da nossa carga!

- a 2 , a 2   .

Resposta

Letra a).

Exercícios de Livros Relacionados

Duas cargas puntiformes, q 1 = 2,0p C e q 2 = - 2,0p C são separadas por 4,0μ m . (a) Qual é o módulo de dipolo deste par de cargas? (b) Represente o par e mostre a direção e o sentido do momento de d
Um elétron que tem uma energia cinética igual a 2,00 × 10 - 16J está se movendo para a direita ao longo do eixo de um tubo de raios catódicos, como mostra a Figura 21-40. Um campo elétrico E → = 2,00
Um elétron é liberado a partir do repouso em um campo elétrico pouco intenso dado por E → = - 1,50 × 10 - 10N / Cy ^ . Depois que o elétron percorre uma distância vertical de 1,0μ m , qual o valor do
Qual é o campo elétrico de um núcleo de Ferro a uma distância igual a 6,00x10 - 10m do núcleo? O número atômico do ferro é igual a 26. Suponha que o núcleo possa ser considerado uma carga puntiforme.
Uma carga puntiforme de +8,75μ C está colada em uma mesa horizontal com atrito desprezível. Ela está atada a uma carga puntiforme de -6,5μ C por um por um fio leve, não condutor, de 2,5c m . Um campo