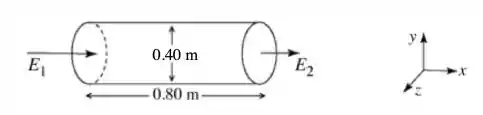
Um campo elétrico não uniforme é dirigido ao longo do eixo em todos os pontos no espaço. A intensidade do campo varia de acordo com , mas não em relação a ou . O eixo de uma superfície cilíndrica imaginária, de de comprimento e de diâmetro, está alinhado paralelo ao eixo , como mostra a figura. Os campos eléctricos e , nas extremidades da superfície cilíndrica, têm magnitudes de e , respectivamente. Qual o valor do fluxo de campo elétrico através de toda a superfície cilíndrica?

a)

b)

c)

d)

e)

Bom... para encontrarmos o fluxo elétrico em uma superfície, precisamos relembrar da Lei de Gauss:

Onde é o vetor de campo elétrico e é o diferencial de área da superfície estudada.

Como se trata de uma superfície cilíndrica, então temos áreas a serem estudadas:

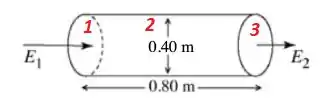
Dessa forma, o fluxo fica:

Se olharmos direitinho e lembrarmos que o produto escalar é dado por:

Onde é o ângulo entre e .

Então podemos concluir que na área , o ângulo é igual (e, portanto, ), fazendo com que seja desconsiderável. E, por outro lado, nas áreas e (que são iguais), temos que .

Assim, temos que o fluxo total é dado por:

Assim, podemos encontrar o fluxo sabendo que ele é a intensidade do campo multiplicada pela área atravessada, ou seja, para o fluxo temos:

Onde é a intensidade do campo elétrico que entra no cilindro e é a área da região circular desse (que é dada por , onde é o raio).

Assim, temos:

E, analogamente, para , temos:

Nesse sentido, substituímos e na equação do passo 1:

Ou, podemos aproximar e dizer que

Entendeu direitinho? Responde aee ;)