Três cargas de estão dispostas como mostra a figura. Cada uma das cargas cria um campo elétrico em um ponto diretamente à frente da carga central e a da mesma.
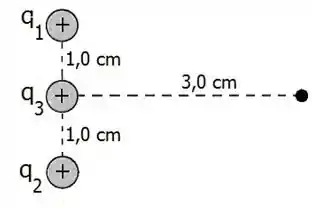
Quais são os três campos , e criados, respectivamente, pelas três cargas? Escreva sua resposta para cada um dos campos como um vetor em função das componentes correspondentes.
O campo elétrico satisfaz o princípio da superposição, logo, existe um “campo resultante” neste ponto dado por . Calcule o valor deste campo.
Passo 1
Para resolver essa questão, vamos adotar o sistema de coordenadas usual:
Lembrando que uma carga genérica produz um campo igual a:
Agora é só analisar os três casos, lembrando que o campo elétrico “sai” das cargas positivas. Vamos para a primeira carga !
Passo 2
Para a carga , teremos duas componentes, uma em , que será positiva, e uma em , que será negativa, dá uma olhada!
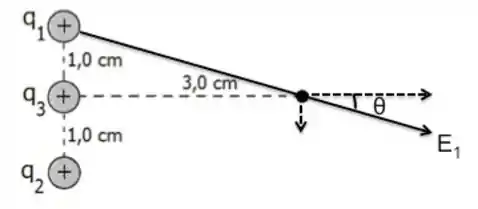
Para determinar o módulo de , basta usar a fórmula, se liga!
Agora é só substituir e determinar as componentes!
A resultante fica:
Agora vamos para !
Passo 3
Para , é bem mais simples, temos apenas a componente . Utilizando a fórmula, temos:
Bora agora pra , que é bem parecida com . Simbora acabar com isso!
Passo 4
Para , temos uma situação bem parecida com , só que agora, a componente será positiva. Temos então:
Vamos primeiro determinar , depois é só substituir!
Substituindo, temos:
A resultante fica:
Passo 5
Para achar a resultante, basta somar os vetores que achamos no item anterior!
Substituindo, temos:
Resposta