UFSJ; Física 3; AV3 – 2ª CH – 2018.2; questão 1b
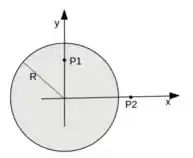
O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionada para fora da página, variando com o tempo , onde é uma constante positiva.
b) Determine o vetor campo elétrico nos pontos e , onde e .
Passo 1
E aí pessoal, tudo bão por aí???
Hoje nós vamos destruir essa questão teórica! Vem comigooo!
O macete dessa questãozita é lembrar que o campo elétrico é definido pela equação obtida no item a).
Ou sejaaa, aqui vai ser o trabalho braçal de aplicar os casos que o enunciado nos deu!
Passo 2
No ponto
Nesse caso, :
No ponto o campo vai apontar no sentido, logo:
No ponto
Nesse caso,
No ponto o campo vai apontar no sentido , logo:
Curtiu a resolução? Responde Aí!!
Resposta
Exercícios de Livros Relacionados
Duas cargas puntiformes, q 1 = 2,0p C e q 2 = - 2,0p C são separadas por 4,0μ m . (a) Qual é o módulo de dipolo deste par de cargas? (b) Represente o par e mostre a direção e o sentido do momento de d
Um elétron que tem uma energia cinética igual a 2,00 × 10 - 16J está se movendo para a direita ao longo do eixo de um tubo de raios catódicos, como mostra a Figura 21-40. Um campo elétrico E → = 2,00
Um elétron é liberado a partir do repouso em um campo elétrico pouco intenso dado por E → = - 1,50 × 10 - 10N / Cy ^ . Depois que o elétron percorre uma distância vertical de 1,0μ m , qual o valor do
Qual é o campo elétrico de um núcleo de Ferro a uma distância igual a 6,00x10 - 10m do núcleo? O número atômico do ferro é igual a 26. Suponha que o núcleo possa ser considerado uma carga puntiforme.
Uma carga puntiforme de +8,75μ C está colada em uma mesa horizontal com atrito desprezível. Ela está atada a uma carga puntiforme de -6,5μ C por um por um fio leve, não condutor, de 2,5c m . Um campo