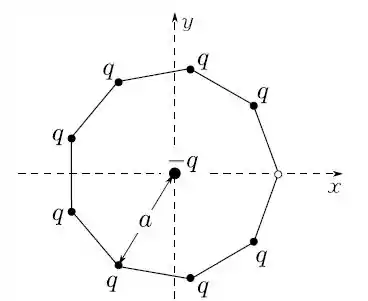
Considere um eneágono (polígono de nove lados) regular, com partículas de carga em cada um de seus vértices, exceto um deles, conforme mostrado na figura. Qual é a força elétrica resultante sobre uma partícula de carga no centro do polígono.
a)
b)
c)
d )
e)
f)
Passo 1
Cara, essa é uma das questões mais sacanas da história porque ela é fácil, mas só se você souber a sacada...
Beleza, ele quer a força elétrica no centro. Vamos decompor os vetores todos e somar? Não! Repare que ele deixou um dos nove lados vazio...
Utilizando a simetria do problema (o polígono é regular, isso quer dizer que os lados e os ângulos são todos iguais) temos que, se puséssemos uma carguinha no espaço que falta, a soma das forças na carga no centro seria zero:
Ou seja, a força que o enunciado pede é dado por
Passo 2
A força que a carguinha faz (ou faria, se nós puséssemos ela lá) nós sabemos calcular:
Isso por que a nossa carguinha atrai a a carga do centro, então a força na carga do centro aponta para a direita () e a distância entre elas é .
Passo 3
Dessa forma, temos que a força que o resto das oito cargas fazem é só trocar o sinal do campo da carguinha:
Resposta
Letra F