Duas cargas são colocadas como indica a Figura abaixo. O módulo da carga é , porém não conhecemos seu sinal e nem o valor da carga . O campo elétrico resultante no ponto aponta para o sentido negativo do eixo .
- Dados a direção e o sentido de , determine os sinais das cargas e
- Determine o valor do módulo da carga
- Calcule o módulo do campo elétrico .
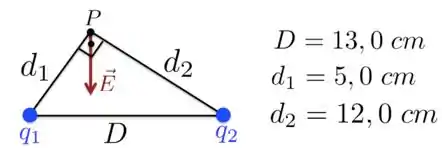
Passo 1
a) É importante que a gente se lembre de que o campo elétrico produzido por cargas positivas é um campo de afastamento e que campos gerados por cargas negativas são campo de aproximação. Ou seja, o campo produzido pela carga positiva tem um vetor que se afasta da carga, enquanto para a negativa, o campo que ela cria tem um vetor que se aproxima dela.
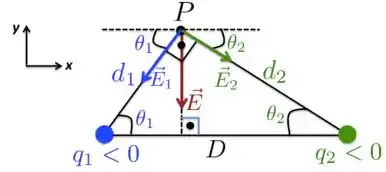
No caso colocado no exercício, como representa vetor campo elétrico resultante no ponto devido às cargas e , então, essas cargas só podem ser negativas. Se qualquer uma dessas cargas for positiva, ou ambas positivas, a direção e/ou o sentido do campo resultante será diferente do que está na Figura acima. Portanto, devemos ter que
como está representado na Figura, com os respectivos campos produzidos no ponto .
Passo 2
b) Agora, como o campo elétrico resultante tem apenas componente na direção , podemos escrever, considerando a geometria lá da Figura, para as direções e :
Uma relação que ajuda a gente bastante aqui vem de notar que, como temos um triângulo retângulo, vale que
que dá o seguinte
Substituindo essa relação trigonométrica que encontramos lá na expressão da direção , chegamos a
Dessa expressão, podemos encontrar o valor de , pois temos os valores da carga e da distância dessa carga até o ponto . Como queremos obter o valor da carga negativa e o valor de e são conhecidos, podemos expressar como:
Da Figura, a gente vê que . Substituindo esse valor e tomando os valores dados no enunciado, temos
Passo 3
c) Substituindo
na expressão que a gente obteve para a direção , obtemos que é dado por
Como , temos que . Substituindo na expressão acima
Colocando os valores dados no exercício, temos