UFF – Física 2 – Provas Antigas – VR – 2022.1 – Questão 8
Na figura, um anel de de raio carrega uma carga uniformemente distribuída sobre ele. Uma carga pontual é colocada no centro do anel. O campo elétrico resultante no ponto é igual a zero, que está no eixo do anel (eixo ) e a de seu centro. A carga pontual , em nanoCoulombs (), está mais próxima de
Dados:
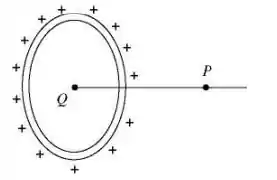
A)
B)
C)
D)
E)
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão queremos descobrir o valor da carga pontual que está localizada no centro do anel de forma que o campo elétrico resultante no ponto seja zero.
Entendido até aí, né? Pois bem... de que forma podemos calcular esse valor de carga?
Concorda que para o campo no ponto ser zero, então a carga deve ser igual a carga ?? Pois é!! Então o valor de é igual ao de , porém com sinal oposto!! Assim:
Em que é o campo gerado pela carga e é o campo gerado pela carga .
Então bora lá descobrir!!!
Passo 2
Bom... primeiramente precisamos saber que o campo elétrico gerado por uma carga pontual é dado por:
Onde é a constante eletrostática (com valor ) e é a distância entre o centro do anel e o ponto .
Passo 3
Dessa forma, da equação do passo 1, temos:
Entendeu direitinho? Responde aee ;)
Resposta
A)