Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação Não Exata - Fator Integrante

Ver Teoria
Exercício 561234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545557585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

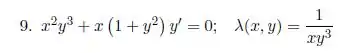
Passo 1

Primeiro de tudo vamos colocar essa equação no formato de uma equação exata.

x 2 y 3 d x + x 1 + y 2 d y = 0

Agora para testarmos o fator integrante devemos multiplicar toda a equação por λ = 1 x y 3 .

x 2 y 3 . 1 x y 3 d x + x 1 + y 2 . 1 x y 3 d y = 0

x d x + 1 + y 2 y 3 d y = 0

M x , y = x

N x , y = 1 + y 2 y 3

Passo 2

Tá tudo bonito e agora vamos testar se essa equação realmente ficou exata.

∂ M ∂ y = 0

∂ N ∂ x = 0

∂ M ∂ y = ∂ N ∂ x

Logo temos realmente uma equação exata e já podemos começar a aplicar o método.

Passo 3

Calculando ∫ M x , y d x

∫ x d x = x 2 2 + g ( y )

Passo 4

Derivando o que obtivemos no passo 2 por y .

∂ x 2 2 + g y ∂ y = g ' ( y )

Passo 5

Comparando o que temos no passo 4 com N ( x , y )

g ' y = 1 + y 2 y 3

Integrando a equação.

g y = ln ⁡ y - 1 2 y 2

Passo 6

Substituindo o passo 5 no que obtivemos no passo 3 teremos a função u x , y .

u = x 2 2 + ln ⁡ y - 1 2 y 2

A nossa solução será dada por u x , y = D

D = x 2 2 + ln ⁡ y - 1 2 y 2

2 D = x 2 + 2 ln ⁡ y - y - 2

Tomando 2 D = C

C = x 2 + 2 ln ⁡ y - y - 2

Resposta

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores