UERJ, Sem Campus, Cálculo III, P1 - Profº Claudio Plinio - 2019.2, Questão 3b
Desenhar as curvas ou superfícies de nível dos seguintes campos escalares.
b.
Passo 1
Olá meu amigo, Yuri aqui e agora iremos resolver essa querida questão. Aqui temos que desenhar superfície de nível de um campo escalar.
Para essa tarefa iremos utilizar nosso amigo GeoGebra, iremos chamar de a nossa querida função e variar seus valores e observar como a nossa função se comporta.
Passo 2
Analisando o que foi feito acima, vemos que nossas superfícies de nível serão esferas de raio
Passo 3
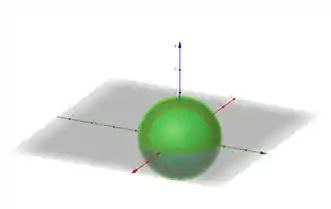
Acima vemos as superfícies de nível para
Resposta
Ver o desenvolvimento.
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores