USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I, Questão 24
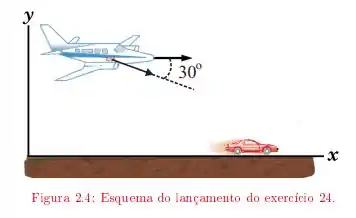
Um avião bombardeiro, a de altitude, voa em perseguição a um carro, no solo, que viaja a . Em dado instante, o avião lança uma bomba com velocidade escalar igual a , fazendo um ângulo de 30◦ com a horizontal. A que distância horizontal do carro deve ser lançada a bomba para que acerte o alvo?
Passo 1
Eaew, belezinha?
Temos que encontrar a que distância horizontal do carro deve ser lançada a bomba para que acerte o alvo. Sabemos que o avião, a de altitude, lança a bomba com velocidade escalar igual a fazendo um ângulo de 30◦ com a horizontal e que o carro viaja a .
Vamos lá!
Passo 2
Primeiro vamos escrever as velocidades em :
.
Temos que a bomba é lançada fazendo um ângulo de 30° com a horizontal, então suas componentes serão:
.
Passo 3
Agora vamos encontrar a velocidade que a bomba terá com relação ao carro, como esse tem velocidade apenas na direção x, temos que
Passo 4
Então, como temos a velocidade, precisamos apenas do tempo de queda para encontrar qual será a distância percorrida horizontalmente pela bomba até atingir o carro. Para encontrar o tempo de queda , temos que nele e e a velocidade , assim
Resolvendo por Bhaskara e escolhendo a solução positiva, pois estamos calculando um instante de tempo, temos que
.
Passo 5
Agora que sabemos o tempo de queda e a velocidade relativa da bomba com relação ao carro, podemos calcular a distância horizontal que ela irá percorrer, sendo essa a distância que o avião deve estar do carro quando lançar a bomba. Essa distância é dada pelo produto entre a velocidade relativa e o tempo de queda:
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
.