Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lançamento Oblíquo

Ver Teoria
Exercício 901234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889919293949596979899100

Enunciado

Livro Halliday, Volume 1, 8ª Edição, Capítulo 4, Seção 6, Exercício 47

(Cap 4 – Ex 47) Um rebatedor golpeia uma bola de beisebol quando o centro da bola está 1,22   m acima do solo. A bola deixa o taco fazendo um ângulo de 45 ° com o solo e com uma velocidade tal que o alcance horizontal (distância até voltar à altura de lançamento) é 107   m .

(a) A bola consegue passar por um alambrado de 7,32   m de altura que está a uma distância horizontal de 97,5   m do ponto inicial?

(b) Qual é a distância entre a extremidade superior do alambrado e o centro da bola quando a bola chega ao alambrado?

Passo 1

Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?

Vamos começar esse exercício com uma dica. Temos que escolher como origem do movimento um ponto que facilite nossa vida. Sendo assim, escolhemos como origem o ponto do solo verticalmente abaixo do ponto de contato entre o taco e a bola. Na ausência de um alambrado, com θ 0 = 45 ° , o alcance horizontal (até a altura de lançamento) é R = 107   m . Queremos saber a que altura do solo estará a bola quando tiver percorrido uma distância horizontal x ' = 97,5   m , mas para isso precisamos conhecer a velocidade inicial. Nós sabemos que a trajetória pode ser descrita pela equação:

y - y 0 = tan ⁡ θ 0 x - g x 2 2 ( v 0 cos ⁡ θ 0 ) 2

Dêem uma olhadinha na figura que representa o problema:

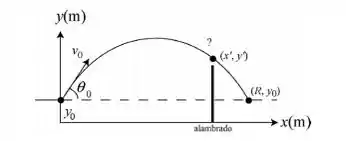
Passo 2

Então, a primeira coisa que devemos fazer, é calcular a velocidade inicial   v 0 . Substuindo o valor do alcance horizontal ( y = y 0     p a r a   x = R )     e do ângulo de lançamento ( θ 0   =   45 ° ) na equação da trajetória, temos:

v 0 = g R sen ⁡ 2 θ 0

v = 9,8 107 sen ⁡ 90 °

Logo:

v = 32,4   m/s

Até aqui tranquilo? Bora continuar que ainda não acabou!

Passo 3

Agora podemos calcular o instante que a bola chega até o alambrado através da relação:

x ' = ( v 0 cos ⁡ θ 0 ) . t '

Logo:

t ' = x ' v o c o s θ 0

t ' = 97,5   m 32,4   m/s cos ⁡ 45 ° = 4,26   s

Passo 4

Agora podemos achar a altura da bola nesse instante através da relação:

s = s 0 +   v 0 t + a t 2 2

y ' =   y 0 + v 0 sen ⁡ θ 0 t ' + a t ' 2 2

Portanto:

y ' = 1,22 + 32,4 sen ⁡ 45 ° 4,26 - 9,8 4,26 2 2

y ' = 9,88   m

Logo, a bola passa pelo alambrado porque ele tem apenas 7,32   m de altura.

Passo 5

Para finalizar, no instante t ' = 4,26   s , momento em que a bola chega no alambrado, a distância entre a extremidade superior do alambrado e o centro da bola é 9,88 m - 7,32   m = 2,56   m .

Ah, como a Física é linda!

Para essa questão é isso pessoal! Bora resolver mais uma?

Resposta

(a) Sim.

(b) 2,56   m

Exercícios de Livros Relacionados

Suponha que o ângulo inicial α 0 da Figura 3.26 seja 42,0 ° e que d seja igual a 3,0 m. Onde o dardo e o macaco se encontrarão, se a velocidade inicial do dardo for a) 12,0 m/s? b) 8,0 m/s?c) O que oc
Galileu mostrou que, se os efeitos da resistência do ar são ignorados, os alcances de projéteis (no mesmo nível) cujos ângulos de projeção diferem de 45°, para mais e para menos, do mesmo valor, são i
Em 1939 ou 1940 , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Za
Os esquiadores experientes costumam dar um pequeno salto antes de chegarem a uma encosta descendente. Considere um salto no qual a velocidade inicial é v 0 =10m / s , o ângulo é θ 0 =9,0 ° , a pista a
Cortina da morte. Um grande asteroide metálico colide com a Terra e abre uma cratera no material rochoso abaixo do solo, lançando pedras para o alto. A tabela a seguir mostra cinco pares de velocidade