[Enunciado comum às Questões 1 e 2]
Uma bola é lançada com velocidade acima da horizontal e leva para atingir a parede.
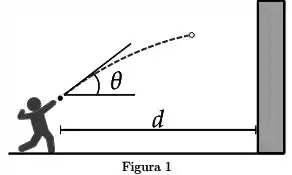
[Questão 2]
Ao atingir a parede, o deslocamento vertical da bola é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Temos um Lançamento Oblíquo e queremos saber qual o deslocamento vertical após (tempo em que a bola atinge a parede).
Então, vamos escrever a equação de movimento na vertical e encontrar a posição em .
Passo 2
Na vertical, temos um Movimento Uniformemente Variado, já que a bola sofre uma aceleração constante (gravidade).
Então, podemos usar essa equação da posição:
Passo 3
Considerando a origem no ponto de partida da bola, temos que:
Temos também a velocidade inicial na vertical, dada pela componente do vetor unitário da velocidade inicial:
Então:
Além disso, usaremos o valor padrão da aceleração da gravidade, lembrando que nosso referencial positivo está para cima, então a gravidade apontando para baixo entra como negativa:
Ficamos então com a seguinte equação para a posição:
Passo 4
Por último, basta encontrar a posição para o instante :
Ou seja, o deslocamento vertical da bola quando ela atinge a parede é aproximadamente:
Ficamos com a alternativa (c).
Resposta
Letra (c)