USP – Física I (Química) – P1 – Questão 5
Ao ser atingida por um taco, uma bola de golfe deixa o solo fazendo um ângulo
de com a horizontal a uma velocidade de . Despreze a resistência do ar.
(a) Qual a altura máxima atingida pela bola?
(b) A que distância do ponto em que foi feita a tacada a bola atinge o solo?
Passo 1
Oi, tudo bem? Vamos começar?
O problema diz que temos uma bola de golfe sendo atingida por um taco. Essa bola adquire então uma velocidade de
E faz um ângulo com o chão de . Antes de mais nada, vamos fazer um esboço dessa situação?
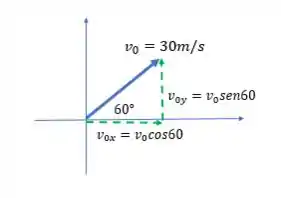
Temos um movimento que pode ser visto separado: em (como MRU) e em (como Queda Livre). O problema pede para descobrirmos a altura máxima que essa bolinha atinge e também o alcance (horizontal)
Mas você se lembra das equações de movimento?
Então a ideia aqui é relacionar os dados do problema (como velocidade inicial, posição inicial, etc), com o que é pedido (altura e alcance) com as equações de movimento! Esse é o segredo! Relacionar sempre o que se quer, com o que se tem!
Mas calma, vou fazer passo a passo com você!
Passo 2
Letra (a): altura máxima da bola
Você precisa lembrar que na altura máxima acontece uma coisa bem legal: a bolinha para de subir momentaneamente! Isso mesmo! Ela atinge a altura máxima quando ela para de subir (a partir desse ponto, ela faz o movimento de retorno ao solo), ou seja, quando sua velocidade vertical é zero
Assim temos os seguintes dados para o movimento vertical:
Das equações de movimento do passo anterior
Vemos que a segunda satisfaz perfeitamente para o que queremos!
Substituindo os valores temos
Tudo bem até aqui?
Passo 3
Letra (b): agora o problema pede para calcularmos o alcance (horizontal) da bola. A única equação para o movimento horizontal é
E temos apenas a velocidade inicial, sendo assim, precisamos encontrar o tempo! E qual seria esse tempo?
O tempo de voo! Tempo de voo é o tempo total em que a bolinha passou no ar. Ou seja, desde o instante em que ela saiu do chão, quando o taco de golfe atingiu ela, até o momento em que ela retorna ao chão, aterrissando
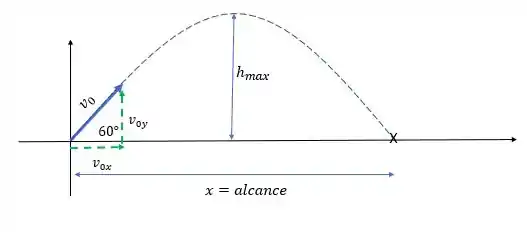
Sendo assim, podemos encontrar o tempo em que a bolinha leva para sair do chão e retornar ao chão , tudo isso usando a equação de movimento para a posição vertical!
Esse é o tempo de voo!
E durante esse tempo todo, a bolinha teve um deslocamento horizontal :
Agora é só substituir
Esse é nosso alcance!
Beleza? Espero ter ajudado!