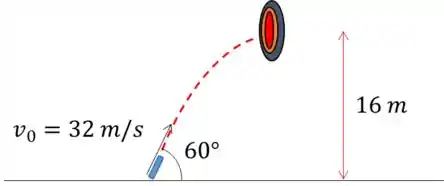
Um projétil é disparado do solo, direcionado a um ângulo de 60° em relação à horizontal com velocidade inicial . No mesmo instante em que é disparado, um alvo é abandonado a de altura, estando na mira da posição inicial do projétil (vide figura). Determine:
a) o vetor posição do alvo, no instante em que ele é abandonado.
b) o vetor posição e o vetor velocidade do alvo no instante em que ele é atingido pelo projétil.
c) Supondo as mesmas condições iniciais, onde apenas o módulo da velocidade inicial do projétil possa ser modificada. Qual será o intervalo possível para (onde é sempre positivo), de forma que o projétil atinja o alvo enquanto este estiver em movimento?
Passo 1
a)
Já sabemos que a componente da posição é , podemos encontrar a componente utilizando a tangente da inclinação.
Logo, o vetor será:
Passo 2
b)
A posição do projétil pode ser obtida pela fórmula do alcance:
A posição do alvo nós já calculamos no item anterior e ela não vai se modificar já que a única força que atua no alvo é a força peso:
No instante em que alvo é atingido teremos:
Agora podemos calcular a posição do alvo:
Logo, o vetor posição do alvo será:
Agora para encontrar o vetor velocidade é mais fácil, só utilizar a fómula:
Passo 3
c)
Vamos fazer o mesmo processo do item anterior.
Posição do alvo:
Posição do projétil:
Instante em que o alvo será atingido:
Para que o projétil atinja o alvo em movimento, o alvo não pode chegar ao chão, logo:
Lembrando que:
Logo temos que:
Resposta
a)
b) ;
c)