Três projéteis A, B e C são lançados da mesma posição inicial do solo com velocidades iniciais de mesmo módulo e que fazem três ângulos diferentes , e , respectivamente com a direção horizontal. Sabendo-se que e que o que pode-se afirmar sobre os tempos que cada projétil leva para atingir novamente o solo?
(a)
(b)
(c)
(d)
(e) Não é possível relacionar os tempos sem saber o módulo da velocidade inicial.
Passo 1
Temos três lançamentos de projéteis que saem com a mesma velocidade.
A única diferença entre eles é o ângulo de inclinação com a horizontal:

Bom, mas qual a relação disso com o tempo de vôo??
Em um Lançamento Oblíquo, olhamos separadamente para o movimento na horizontal e na vertical.
Na horizontal, como não temos nenhuma força atuando, o corpo realiza um movimento uniforme com velocidade constante.
Mas na vertical, o corpo realiza um lançamento vertical (aceleração constante).
E daí?
O tempo de vôo está relacionado como movimento na vertical, pois quando o corpo volta à altura do chão o “vôo” acaba hahah.
Ainda não entendi...
Então, como a aceleração é sempre a mesma, quanto maior for a velocidade na vertical para cima , mais tempo o corpo leva subindo até que sua velocidade chegue a zero :
Assim, ele alcança uma altura maior e também demora mais para retornar ao chão.
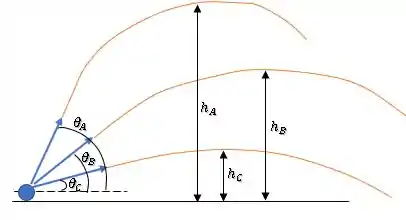
Logo, o que demora mais tempo para alcançar o chão é o vetor velocidade mais inclinado para cima (maior valor de “”), inclinação . Ou seja, o tempo para é maior que o tempo para , que por sua vez, é maior que o tempo para :
Resposta
Letra (d)