UFRJ – Física 1 – P1 – 2019.2 – Questão 7
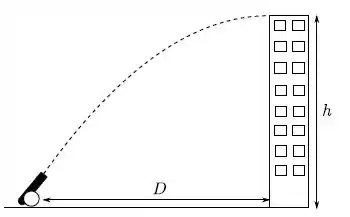
Um canhão encontra-se a uma distância horizontal de uma torre cujo topo está a uma altura . Para que uma bala disparada pelo canhão atinja o topo da torre horizontalmente, como mostra a figura, a tangente do ângulo de disparo deve ser:
Passo 1
Vamos lá! Ele quer descobrir a tangente do ângulo. Se liga na figura!
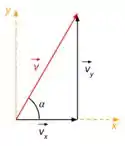
Fazendo a decomposição do vetor , temos
Se queremos achar a , só precisaremos fazer a razão
Passo 2
Podemos lembrar que a altura máxima atingida é dada por
E o tempo que o projétil demora para atingir esta altura é
Passo 3
O tempo que o objeto demora para atingir a altura máxima é o mesmo tempo que o objeto demora para percorrer a distância horizontal. Assim podemos escrever
Portanto
Encontramos que a alternativa correta é a letra (a).
Resposta
Exercícios de Livros Relacionados
Suponha que o ângulo inicial α 0 da Figura 3.26 seja 42,0 ° e que d seja igual a 3,0 m. Onde o dardo e o macaco se encontrarão, se a velocidade inicial do dardo for a) 12,0 m/s? b) 8,0 m/s?c) O que oc
Galileu mostrou que, se os efeitos da resistência do ar são ignorados, os alcances de projéteis (no mesmo nível) cujos ângulos de projeção diferem de 45°, para mais e para menos, do mesmo valor, são i
Em 1939 ou 1940 , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Za
Os esquiadores experientes costumam dar um pequeno salto antes de chegarem a uma encosta descendente. Considere um salto no qual a velocidade inicial é v 0 =10m / s , o ângulo é θ 0 =9,0 ° , a pista a
Cortina da morte. Um grande asteroide metálico colide com a Terra e abre uma cratera no material rochoso abaixo do solo, lançando pedras para o alto. A tabela a seguir mostra cinco pares de velocidade